Властивості змішаного добутку.
6.2.1. Геометричний зміст змішаного добутку.
Змішаний добуток за абсолютною величиною дорівнює об’єму паралелепіпеда, побудованого на векторах  і
і  , як на суміжних ребрах.
, як на суміжних ребрах.
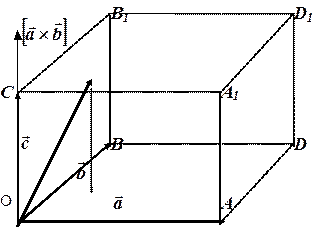
Відобразимо на малюнку векторний добуток векторів  . За означенням векторного добутку його довжина дорівнює площині паралелограма, побудованого на
. За означенням векторного добутку його довжина дорівнює площині паралелограма, побудованого на 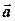 і
і 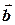 як на суміжних ребрах. В даному випадку:
як на суміжних ребрах. В даному випадку: 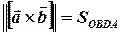 . Тоді, скалярний добуток
. Тоді, скалярний добуток 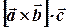 , за означенням скалярного добутку, дорівнює добутку довжин цих векторів на
, за означенням скалярного добутку, дорівнює добутку довжин цих векторів на 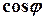 .
.

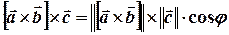
||
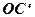
Але відрізок 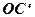 є ні чим іншим як висотою паралелепіпеда
є ні чим іншим як висотою паралелепіпеда 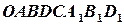 . Змішаний добуток
. Змішаний добуток 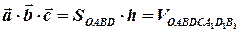 , що і треба було довести.
, що і треба було довести.
6.2.2. Критерій компланарності векторів і точок.
Вектори 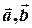 і
і 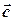 звуться компланарними, якщо після зведення до спільного початку вони лежать в деякій одній і тій самій площині.
звуться компланарними, якщо після зведення до спільного початку вони лежать в деякій одній і тій самій площині.
Теорема (критерій компланарності трьох векторів). Три вектори компланарні тоді і тільки тоді, коли їх змішаний добуток дорівнює нулю.
Доведення. Якщо три вектори компланарні, то вектор 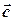 потрапляє в площину
потрапляє в площину 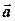 і
і 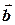 . Отже паралелепіпед
. Отже паралелепіпед 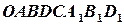 вироджується: він не має висоти, тобто його висота
вироджується: він не має висоти, тобто його висота 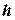 дорівнює нулю, його об’єм теж дорівнює нулю, а з цього випливає, що змішаний добуток теж дорівнює нулю.
дорівнює нулю, його об’єм теж дорівнює нулю, а з цього випливає, що змішаний добуток теж дорівнює нулю.
Нехай є деяка сукупність точок. Будемо називати ці точки компланарними, якщо усі вони лежать в деякій, одній і тій самій, площині.
Теорема (критерій компланарності чотирьох точок). Чотири точки 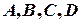 компланарні тоді і тільки тоді, коли
компланарні тоді і тільки тоді, коли 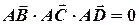 .
.
Доведення — виконати самостійно, спираючись на критерій компланарності трьох векторів.
6.2.3. Алгебраїчні властивості змішаного добутку.
Теорема. Змішаний добуток має властивості однорідності та аддитивності по кожному з векторів-множників, тобто:
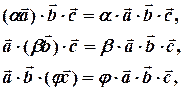 ( однорідність)
( однорідність)
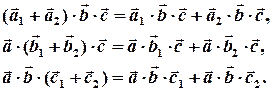 ( адитивність)
( адитивність)
Доведення — виконати самостійно, спираючись на відповідні властивості скалярного і векторного добутків.
Дата добавления: 2021-05-28; просмотров: 575;











