Точки і прямі лінії на площині.

<18 19 202122 23 24 >

7.1.1. Відстань між двома точками.

Формула відстані між двома точками або, що те саме, довжини відрізка є безпосереднім наслідком теореми Піфагора і виведена в §1:

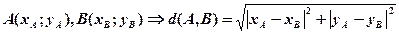7.1.2. Відстань від точки до прямої.

При знаходженні відстані від точки до прямої можна було б, перекладаючи означення відстані на аналітичну мову: скласти рівняння перпендикуляра через дану точку до даної прямої , знайти точку перетину його з даною прямою і за формулою відстані між двома точками знайти відстань від даної точки до точки перетину перпендикуляру з даною прямою. Але це можна зробити значно елегантніше. Розглянемо малюнок:

З рівняння прямої дуже легко можна знайти координати скількох завгодно точок цієї прямої. Нам потрібна одна і навіть не конкретна точка, а те, що ми можемо визначити її координати; нехай це буде 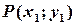. Тоді рівняння прямої можна перетворити до виду 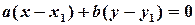, більш точно: 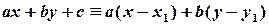. Нормальний вектор прямої 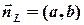можна вважати приєднаним до точки 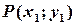. Тепер підставимо координати даної точки 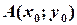в ліву частину рівняння, отримаємо вираз:

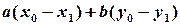Побачимо фігури за числами: цей вираз є не що інше, як скалярний добуток

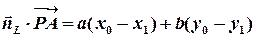який, за означенням, дорівнює

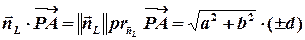звідки остаточно маємо

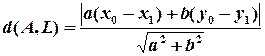7.1.3. Відстань між двома паралельними прямими.

Відстанню між двома множинами називається відстань між парою найближчих точок, одна з яких належить одній, а інша другій з даних множин. Отже, якщо множини перетинаються, тобто мають спільні точки, то відстань між ними, за означенням, дорівнює 0. Розглянемо випадок, коли прямі задані загальними рівняннями:

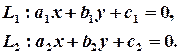
Умовою паралельності прямих є пропорційність відповідних коефіцієнтів біля змінних, в іншому випадку прямі перетинаються і відстань між ними дорівнює 0. Якщо прямі паралельні, то їх рівняння множенням (або діленням) на певні числа можуть бути приведені до виду:

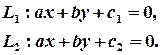
Тепер, використовуючи міркування, аналогічні до проведених в п. 7.1.2, отримуємо формулу відстані між паралельними прямими:

.

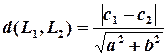Вправа. Розглянути випадок задання прямих рівняннями з кутовим коефіцієнтом і вивести формулу відстані між прямими.

7.1.4. Взаємне розташування точок відносно прямої.

Точка належить прямій 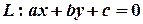тоді і тільки тоді, коли її координати задовольняють рівняння прямої. Якщо є дві точки 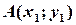і 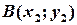і вони обидві не належать прямій, то вони або можуть знаходитись по один, або по різні боки від прямої. Коли саме має місце один з цих випадків, визначають міркування, пов’язані з лінійними нерівностями і півплощинами (див. § 2 ). Пряма 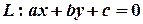розділяє площину на дві півплощини; усі точки однієї півплощини задовольняють нерівність 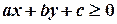, іншої півплощини – нерівність 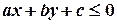. Звідси маємо правило: якщо при підстановці координат точок в ліву частину рівняння, отримано числа одного знаку, то точки розташовані по один бік від прямої, інакше – по різні.

<18 19 202122 23 24 >

Дата добавления: 2021-05-28; просмотров: 306;