Координатне подання змішаного добутку.
Принципово питання про координатне подання змішаного добутку “знімається” самим означенням змішаного добутку: це поняття є похідним від понять скалярного і векторного добутків, для яких координатне подання дано у попередніх лекціях. Дійсно, нехай вектори 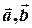 і
і 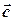 задані своїми координатами:
задані своїми координатами:
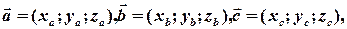
тоді
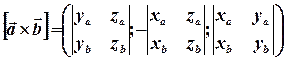 .
.
Звідси
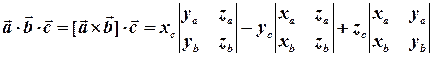 .
.
Якщо в отриманому виразі розкрити присутні в ньому визначники, то ми отримаємо досить громіздкий вираз. З ним незручно мати справу при виконанні проміжних перетворень і міркувань. Але при уважному погляді ми побачимо визначник третього порядку (див. §2), що дозволяє подати змішаний добуток у компактному і красивому вигляді. Нагадаємо, що за означенням, визначник третього порядку – визначник квадратної матриці третього порядку – обчислюється за формулою
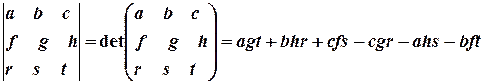 .
.
Теорема (про координатне подання змішаного добутку). Нехай вектори 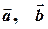 і
і 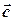 задані своїми координатами:
задані своїми координатами:
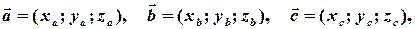
тоді змішаний добуток 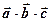 обчислюється за формулою:
обчислюється за формулою:
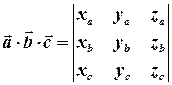 .
.
Доведення. Ми знаємо, що векторний добуток при заданих координатах векторів-множників обчислюється наступним чином:
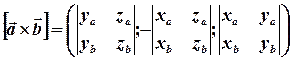 .
.
Відомо, що скалярний добуток дорівнює сумі добутків однойменних координат векторів-множників. Отже, змішаний добуток буде дорівнювати:
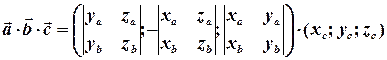
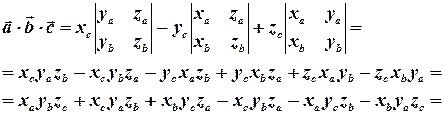
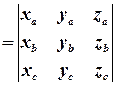 .
.
Приклад. Нехай 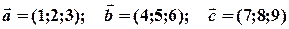 . Тоді
. Тоді
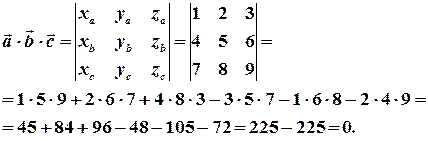
(отже, вектори 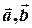 і
і 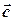 - компланарні).
- компланарні).
Поєднуючи критерій компланарності трьох векторів з формулою координатного подання змішаного добутку, отримуємо: якщо вектори 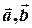 і
і 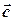 задані своїми координатами:
задані своїми координатами: 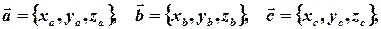 то необхідною і достатньою умовою компланарності цих векторів є співвідношення:
то необхідною і достатньою умовою компланарності цих векторів є співвідношення:
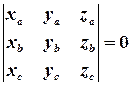 ,
,
тобто рівність нулю визначника третього порядку, який складено з координат векторів 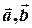 і
і 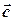 .
.
Дата добавления: 2021-05-28; просмотров: 598;











