Точки і прямі в просторі.

Особливість сумісного розгляду точок і прямих в просторі порівняно з розглядом точок і прямих на площині міститься в одному питанні: відстань від точки до прямої. Означення відстані незмінне – це довжина перпендикуляра, опущеного з точки на пряму. До речі, основа перпендикуляра, опущеного з точки на пряму, – це проекція точки на пряму. Хитрість у знаходженні проекції даної точки на дану просторову пряму полягає в тому, що опускати перпендикуляр з точки на пряму треба не за допомогою прямої, а за допомогою площини. З пропозицією обміркувати цю тезу, пропонуємо нарис технології знаходження проекції точки на пряму.

Нехай є точка 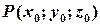і пряма 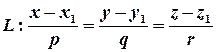. Проводимо площину через точку 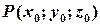перпендикулярно до прямої :

.

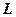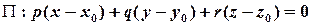Перетинаємо пряму з площиною :

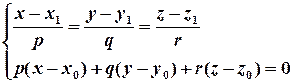
Точка перетину – розв’язок системи – і є проекцією даної точки на дану пряму. Далі залишається скористатися формулою відстані між двома точками.

Безумовно, можна відшукати елегантний спосіб знаходження відстані від точки до прямої без знаходження проекції точки на пряму. Для цього треба мати здібність до просторового уявлення і володіти в достатньому степені арсеналом векторної алгебри. Пропонуємо бажаючим зробити це в якості вправи.

Також для самостійного опрацювання пропонуємо розглянути випадок, коли пряма 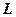задана загальним рівнянням.