Скалярний добуток векторів, його обчислення і застосування.

3.5.1. Означення і властивості скалярного добутку.

Скалярний добуток двох векторів можна ввести (і це можна побачити, зазирнувши в різні підручники) кількома еквівалентними способами.

Означення (скалярного добутку — І). Скалярним добутком двох векторів називається добуток довжини першого вектора і проекції другого вектора на напрямок першого вектора:

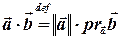Для формулювання другого означення введемо позначення 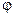кута між векторами 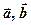(вважаємо при цьому, що дані вектори зведені до спільного початку).

Означення (скалярного добутку — ІІ).

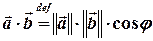Наведені означення, очевидно, еквівалентні між собою, оскільки має місце співвідношення:

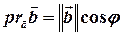
(довести подану рівність самостійно, виходячи з відповідного малюнка).

Теорема ( про властивості скалярного добутку). Скалярний добуток векторів має властивості комутативності, однорідності та адитивності:

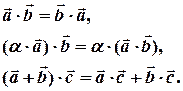
Доведення безпосередньо випливає з означення скалярного добутку та властивостей проекцій (розгорнуте доведення виконати самостійно).

Теорема ( координатне подання скалярного добутку). Нехай є вектори 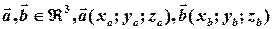. Тоді:

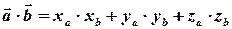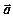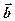Доведення.Розкладемо вектори і за одиничним базисом:

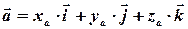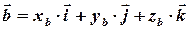Далі залишається скористатися властивостями комутативності, однорідності та адитивності скалярного добутку (продовжити доведення самостійно).

3.5.2. Застосування скалярного добутку.

3.5.2.1.Рівняння прямої лінії, що проходить через задану точку

перпендикулярно заданому вектору.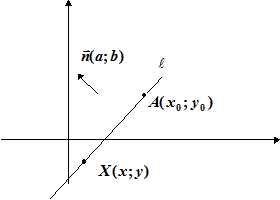

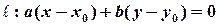
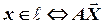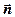
3.5.2.2.Рівняння площини, яка проходить через задану точку перпендикулярно до заданого вектора.

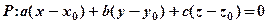
3.5.2.3.Доведення теореми косинусів за допомогою скалярного добутку.

Теорема косинусів. В

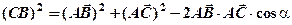
Доведення. Нехай у трикутника 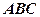маємо: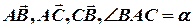

Вектор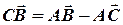

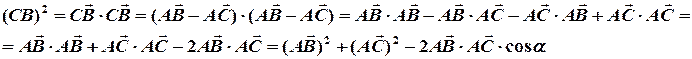
Якщо 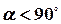, cos 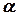— додатний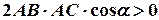, то , то .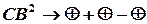

Якщо 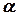- гострий, то .

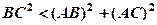Якщо 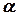- тупий, соs 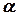<0, то 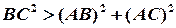, 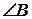- гострий.

3.5.2.4.Геометричний образ лінійної нерівності.

Лінійне рівняння з двома змінними 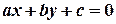визначає пряму лінію на координатній площині (з трьома змінними — 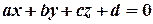— площину в просторі). Нехай 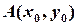— деяка точка на цій прямій лінії, тоді можна загальне рівняння перетворити до вигляду:

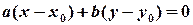
Це рівняння виражає таку умову:

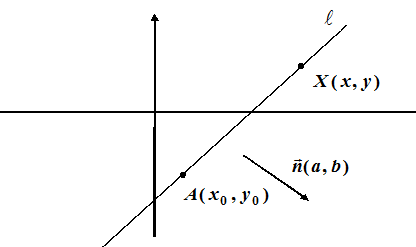
Умова: точка 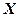належить прямій 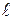тоді і тільки тоді, коли вектор .

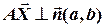Ліва частина останнього рівняння є скалярний добуток саме вказаних векторів ( 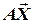і ).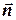

З означення скалярного добутку ( 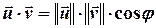) випливає, що нерівність 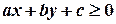задовольняють ті і тільки ті точки площини, радіус-вектор яких від точки А, що належить прямій 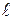утворює з нормальним вектором 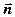гострий кут .

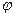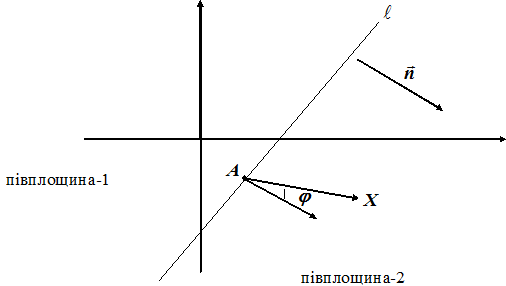
Точка 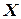задовольняє нерівність 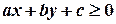, коли радіус-вектор 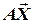утворює гострий кут 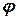з нормальним вектором 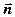. Отже, множиною розв’язків лінійної нерівності 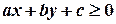- є півплощина -1.

Аналогічно, множиною розвязків нерівності 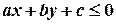є протилежна півплощина -2.

Приклад.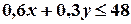

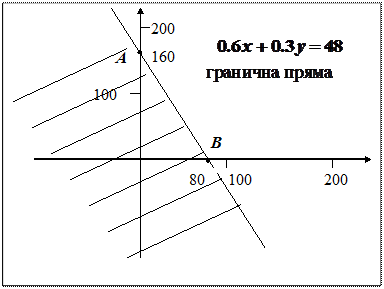
Для визначення того, яку саме півплощину визначає нерівність, можна скористатися способом пробних точок. Беремо будь-яку точку, і якщо вона задовольняє нерівність, то саме цю півплощину визначає нерівність, якщо не задовольняє, — то іншу (протилежну) півплощину:

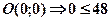
це правильна нерівність, отже, нерівність 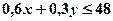визначає ту півплощину, у якій знаходиться точка .

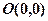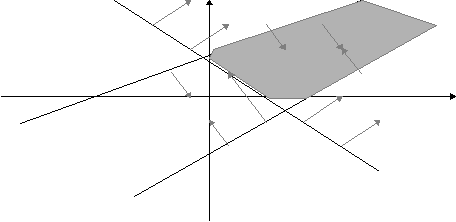
Якщо ми розглядаємо систему з кількох нерівностей, то множиною розв’язків цієї системи є перетин відповідних півплощин, тобто це є така множина точок, які потрапляють в кожну з півплощин:

<8 9 101112 13 14 >

Дата добавления: 2021-05-28; просмотров: 619;