Математична модель задачі лінійного програмування.

<10 11 121314 15 16 >

Ми будемо розглядати задачі пошуку екстремуму (мінімуму або максимуму), лінійної функції за умов, які є лінійними нерівностями або рівняннями, інакше кажучи, лінійні оптимізаційні задачі. Загальні методи розв’язання таких задач вивчаються дисципліною, яка зветься лінійне програмування (ЛП), а самі задачі — задачами лінійного програмування (ЗЛП). ЛП є, у свою чергу, підрозділом іншої дисципліни, що має назву математичне програмування.

Методику розв’язання ЗЛП малих розмірностей ми розглянемо на прикладі двовимірної ЗЛП:

4.1.1. Задача планування виробництва в умовах обмежених ресурсів.

Деяка фірма випускає пилососи і вентилятори. Серед матеріалів, потрібних для виготовлення виробів, “критичними” є мідний дріт і трансформаторне залізо (“критичні” - означає, що саме ці матеріали знаходяться в обмеженій кількості і саме вони визначають обсяг продукції). Для виготовлення одного пилососа потрібно 0,6 кг мідного дроту і 0.3 кг трансформаторного заліза, одного вентилятора - 0,3 кг мідного дроту і 0,2 кг трансформаторного заліза. В наявності є 48 кг мідного дроту і 30 кг трансформаторного заліза. Чистий прибуток від реалізації одного пилососа складає 120, а одного вентилятора – 70 умовних грошових одиниць. Треба визначити план випуску пилососів і вентиляторів (кількість пилососів і вентиляторів, яку потрібно виробити) для якого вистачило б запасів дроту і заліза і якому відповідав би максимальний прибуток.

4.1.2. Формалізація задачі планування виробництва в умовах обмежених ресурсів.

Вводимо змінні: 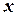- кількість пилососів, 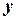- кількість вентиляторів. Тоді потрібна кількість дроту та заліза буде такою:

	дріт	залізо
х - кількість пилососів у - кількість вентиляторів	0,6×х 0,3×у	0,3×х 0,2×у

(для одного потрібно 0,6 кг, а для х=0,6×х).

Сумарна кількість дроту та заліза не повинна перевищувати їх запасів. Звідси отримуємо умови:

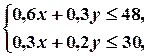
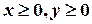Цільова функція задачі - це функція прибутку від реалізації х пилососів і у вентиляторів. Цю функцію ми назвемо :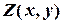

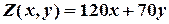Прибуток (функцію 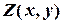) ми хочемо максимізувати; отже маємо задачу пошуку екстремуму, а саме, максимуму (max), лінійної функції за умов, які є лінійними нерівностями, тобто лінійну оптимізаційну задачу.

4.1.3. Загальна структура задачі лінійного програмування.

Математична модель задачі ”Планування виробництва” має вигляд:

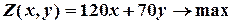(цільова функція)

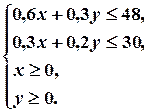
(прямі обмеження - умова невід’ємності змінних)

(непрямі обмеження)

Розв’язання ЗЛП.

4.2.1. Побудова допустимої області ЗЛП.

Пригадаємо ( див. попередній параграф), що множиною розв’язків лінійної нерівності 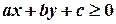є півплощина . Якщо ми розглядаємо систему з кількох нерівностей, то множиною розв’язків цієї системи є перетин відповідних півплощин, тобто це є така множина точок, які потрапляють в кожну з півплощин.

Почнемо розгляд ЗЛП з побудови зображення на координатній площині допустимої області (множини) ЗЛП — множини розв’язків системи лінійних нерівностей, у якій об’єднано непрямі і прямі умови ЗЛП.

Зображення множини розв’язків СЛН будуємо за схемою:

· замінюємо в першій нерівності знак нерівності на знак = і отримуємо лінійне рівняння, яке визначає пряму лінію на координатній площині;

· креслимо цю пряму лінію (вона є границею півплощини, яка є множиною розв’язків першої нерівності);

· вибираємо одну, яку завгодно, точку з однієї (якої-небудь) з півплощин, на які розбила площину накреслена пряма; підставляємо координати вибраної точки у першу нерівність; якщо нерівність справджується, то множиною розв’язків нерівності буде та півплощина, де лежить вибрана точка, якщо ні, - інша (“протилежна”) півплощина (часто буває зручно за “пробну” точку брати точку 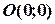- початок координат);

· описані дії виконуємо з кожною із нерівностей;

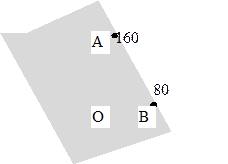
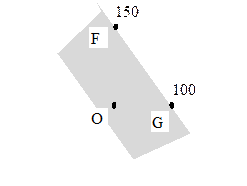
· шукана допустима множина ЗЛП є перетином всіх (у нашому випадку чотирьох) півплощин; геометрично - це є многокутник.

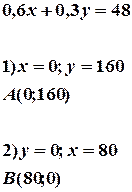
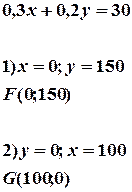
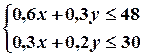
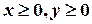
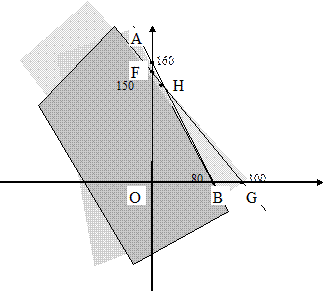
Бачимо, що геометричне місце точок, які задовольняють кожну з нерівностей, утворюють чотирикутник 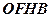. В ньому нам відомі координати всіх вершин, крім точки .

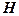Координати точки 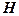знаходимо за такою схемою:

· визначаємо з малюнка, на перетині граничних прямих яких нерівностей знаходиться ця вершина;

· утворюємо систему двох рівнянь з двома невідомими, беручи рівняння двох прямих, визначених на попередньому кроці;

· розв’язуємо утворену систему лінійних рівнянь; знайдений розв’язок - це і є шукані координати розглядуваної вершини.

Обчислюємо за наведеною схемою координати вершини .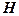

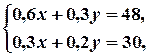
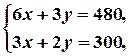
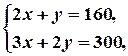
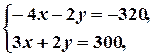
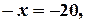
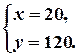
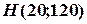
* 10 * 10

: 3

*(-2)

Допустима множина побудована і координати всіх вершин відповідного многокутника обчислені.

4.2.2. Пошук оптимального допустимого розв’язку.

Почнемо пошук оптимального розв’язку ЗЛП. Для цього залучимо до розгляду цільову функцію:

.

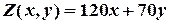Розглядувана ЗЛП полягає у знаходженні точки з допустимої множини, у якій цільова функція набуває найбільше значення серед усіх значень в усіх допустимих розв’язках, тобто, серед значень в усіх точках допустимої множини.

Нехай r - це деяке дійсне число, яке ми будемо розглядати як значення (у якійсь точці) цільової функції. З огляду на таку інтерпретацію ми будемо називати число r рівнем цільової функції (отже, нам треба знайти точку допустимої множини з найбільшим рівнем цільової функції).

Нехай r - це деякий рівень. Множина точок 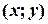координатної площини з даним рівнем r цільової функції, тобто, для яких

,

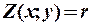зветься лінією рівня цільової функції. У нашому конкретному випадку це буде пряма лінія з рівнянням

.

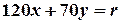Зобразимо на спільному малюнку допустиму множину і декілька ліній рівня цільової функції, а саме , , :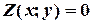

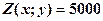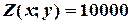Всі лінії рівня паралельні, вони мають спільну нормаль, тобто спільний нормальний вектор. Для “конкретизації” цього вектора можна скористатися коефіцієнтами біля невідомих у якому-небудь з рівнянь:

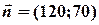
Один з напрямків перпендикуляра, і як раз той, що визначається вибраним нами вектором, перпендикулярним (чому ?), до ліній рівня є напрямком зростання, інший - напрямком спадання цільової функції.

Якщо якась лінія рівня перетинає допустиму множину ЗЛП, це означає, що у допустимій множині є точки, у яких цільова функція набуває відповідного значення.

Отже, для того, щоб знайти оптимальний розв’язок ЗЛП, треба лінію рівня цільової функції пересувати паралельно у напрямку зростання доти, поки вона ще перетинає допустиму множину.

Остання точка перетину лінії рівня з допустимою областю ЗЛП („точка прощання”) є оптимальним розв’язком ЗЛП:

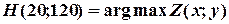
Отже оптимальний план виробництва пилососів і вентиляторів: 20 пилососів і 120 вентиляторів.

4.3. Загальні властивості оптимального розв’язку ЗЛП.

4.3.1. Основна властивість оптимального розв’язку ЗЛП.

Геометричні міркування дають змогу сформулювати загальне положення, що визначає місцезнаходження оптимальної точки ЗЛП у допустимій множині.

Допустима множина ЗЛП, як перетин півплощин, є опуклим многокутником. Отже, якщо взяти яку-небудь внутрішню (тобто яка не лежить на границі) точку допустимої множини і якщо провести через цю точку лінію рівня, то цю лінію рівня можна, хоч трохи, зрушити як у напрямку зростання, так і в напрямку спадання. І вона все ще буде перетинати допустиму множину. Таким чином, внутрішня точка допустимої множини ЗЛП не може бути оптимальним розв’язком ЗЛП.

Звідси висновок: оптимальний розв’язок ЗЛП, якщо він існує, є вершиною допустимої множини ЗЛП.

4.3.2. Знаходження оптимального розв’язку ЗЛП методом перебирання вершин допустимої області.

Інколи, через неточності малюнка, важко визначити, яка саме вершина допустимої області є точкою екстремуму цільової функції ЗЛП. В таких випадках треба обчислити значення цільової функції в декількох “підозрілих” точках:

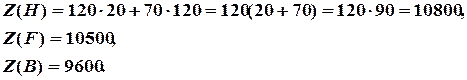
Точка максимуму — .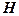

4.3.3. Класифікація можливостей щодо “вмісту” множини оптимальних розв’язків ЗЛП.

У загальному випадку можна виділити три якісно різних випадки щодо “вмісту” множини оптимальних розв’язків ЗЛП. Ці випадки однакові як для задачі мінімізації, так і для задачі максимізації. Обмежимось розглядом задачі максимізації.

1) Множина оптимальних розв’язків порожня (ЗЛП не має оптимального розв’язку).

1а) Допустима множина ЗЛП порожня (система обмежень є несумісною).

1б) Допустима множина необмежена у напрямку зростання цільової функції.

2) Множина оптимальних розв’язків містить один-єдиний елемент (точку). В такому випадку оптимальний розв’язок ЗЛП неодмінно є вершиною допустимої області. Прикладом такої ситуації може служити розглянута задача.

3) Множина оптимальних розв’язків нескінчена; це буває в тому випадку, коли лінія рівня паралельна якійсь стороні допустимої множини. Тоді множина оптимальних розв’язків складається із всіх точок цієї сторони, причому ця сторона може бути як відрізком, так і променем:

3а)

3б)

Лінія рівня паралельна стороні допустимої множини.

<10 11 121314 15 16 >

Дата добавления: 2021-05-28; просмотров: 502;