Точки та їх радіус-вектори.

<9 10 111213 14 15 >

Вектор, який сполучає початок координат (декартової площини або декартового простору) з якою-небудь точкою (цієї площини або простору), називається радіус-вектором цієї точки.

Точки та їх радіус-вектори знаходяться між собою у взаємно однозначній відповідності: кожна точка має свій радіус-вектор і радіус-вектори двох різних точок також різні. Арифметичні операції над векторами вже введені. Це дає змогу ввести арифметичні операції над точками:

нехай 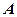– деяка точка, 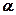– деяке число, тоді 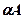– це точка, радіус-вектором якої є радіус-вектор точки 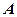, помножений на число :

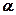нехай 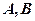– деякі точки, 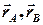– їх радіус-вектори; тоді 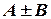– це точка, радіус-вектором якої є вектор :

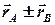нехай 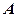– деяка точка, 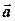– деякий вектор 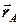– радіус-вектор точки 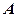; тоді 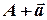– це точка, радіус-вектор якої дорівнює :

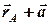Таким чином, додати вектор до точки – це означає перенести дану точку на даний вектор. Ця операція дозволяє без додаткових перетворень, пов’язаних, наприклад, з використанням формули для координат середини відрізку знаходити точку, симетричну даній точці відносно даної прямої. Нехай треба знайти точку 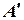, симетричну точці 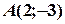відносно прямої 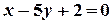. Тоді 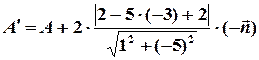, де 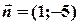– нормальний вектор прямої. Отже, (-5.45; 34.25).

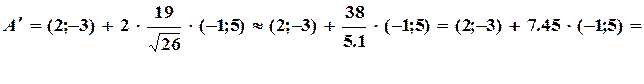<9 10 111213 14 15 >

Дата добавления: 2021-05-28; просмотров: 436;