Координатне подання арифметичних операцій над векторами.

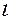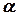Лема (про властивості проекцій векторів). Для будь-якої числової осі , для будь-якого вектора і для будь-якого дійсного числа виконується:

;

для будь-якої числової осі 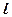та для будь-яких векторів і 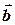виконується:

.

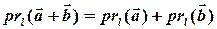Те ж саме вірно й для проекції вектора на напрямок іншого вектора.

Доведення очевидно випливає з розгляду малюнку:

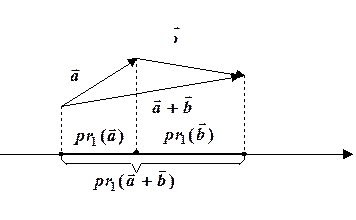
Теорема (про координатне подання арифметичних операцій над векторами). Для будь-якого вектора 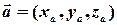і будь-якого дійсного числа 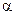виконується:

;

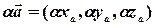для будь-яких векторів 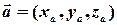і 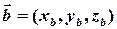виконується:

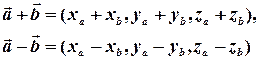
(формули подано для випадку простору).

Довести теорему самостійно, виходячи з означень координат вектора, операцій над векторами та використовуючи попередню лему.

Поняття одиничного декартового базису. Розкладення векторів за базисом.

Означення (одиничного декартового базису). Пара (у випадку площини) або трійка (у випадку простору) векторів одиничної довжини, колінеарних і співнаправлених координатним осям, називаються одиничним декартовим базисом відповідно декартової площини або декартового простору.