Линейные однородные дифференциальные уравнения второго порядка с постоянным коэффициентом.

Уравнение вида F(х;у;у^/;у^//) = 0 называется дифференциальным уравнением второго порядка, где у = у(х) – искомая неизвестная функция, у^/ = у^/(х) и у^// = у^//(х) – ее производные по х первого и второго порядка, а F - заданная функция переменных х, у, у^/,у^//.

Функция φ(х), х 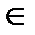(а;b), называется решением дифференциального уравнения F(х;у;у^/;у^//) = 0, если она имеет производные φ^/(х) и φ^//(х) и если для любого х 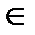(а;b) справедливо равенство F ( х; φ(х); φ^/(х); φ^//(х)) = 0

Дифференциальные уравнениявида: 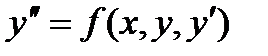.- называется уравнением, разрешением относительно второй производной, где f – заданная функция переменных х, у, у^/ .

Дифференциальные уравнениявида у^// + ру^/ + qy = f(x) где р и q – некоторые числа, называется линейными дифференциальными уравнениями второго порядка.

Функция f(х) называется свободным членом или правой частью уравнения

у^// + ру^/ + qy = f(x).

Если f(х) 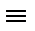0, то дифференциальное уравнение называется линейным однородным уравнением . Оно имеет вид у^// + ру^/ + qy = 0

Пример:

Найти все решения уравнения у^// -y = 0

Решение:

Легко проверить, что функция у = е^х является решением данного уравнения. Аналогично проверяется, что и функция у = е^-х является решением уравнения. Покажем, что при любых С₁ и С₂ функция у = С₁е^х + С₂е^-х является решением уравнения у^// -y = 0. Имеем:

у^/ = С₁е^х - С₂е^-х

у^// = С₁е^х + С₂е^-х = у

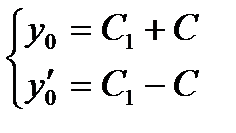
С₁ =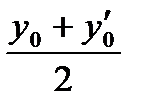

С₂ =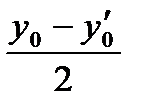

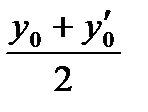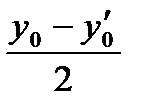y = ₁е^х + е^-х является решением задачи Коши

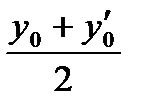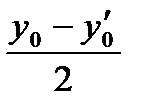В силу единственности решения задачи Коши φ(х) = ₁е^х + е^-х

Таким образом у = С₁е^х + С₂е^-х задает общее решение уравнения.