Операции над множествами и их свойства.

Графы.

Элементы графов.

Виды графов и операции над ними.

Обоснование основных понятий комбинаторики: факториал, перестановки, размещения, сочетания.

Цели: создание благоприятных условий для изучения определение предела последовательности и предела функции; познакомить с правилами вычисления пределов функции в точке и на бесконечности, понятия числового ряда; ввести понятие сходимости и расходимости рядов; познакомить с признаком Даламбера; познакомить с формулой разложения степенных функций в ряд Маклорена; понятия множество и его элементов; познакомить с операциями над множествами и их свойствами; ввести понятие графа и элементов графа; познакомить с видами графов и операциями над ними; основных понятий комбинаторики: факториал, перестановки, размещения и сочетания.

Ход занятия:

Предел числовой последовательности.

Рассмотрим для числовые последовательности – (у_n) и (x_n).

(у_n): 1, 3,5, 7, 9, … 2n – 1, …;

(x_n): 1,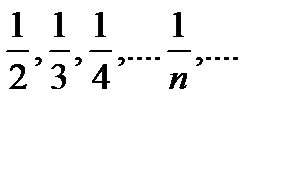

Изобразим члены этих последовательностей точками на координатной прямой.

У

0 0,25 0,5 1

Замечаем, что члены последовательности (x_n) как бы «сгущаются» около точки 0 – говорят последовательность сходятся , а у последовательности (у_n) такой точки сгущения нет – и говорят, что последовательность расходится.

Определение: Число b называется пределом последовательности (у_n), если в любой заранее выбранной окрестности точки b содержится все члены последовательности, начиная с некоторого номера.

Пишут так: у_n→b или 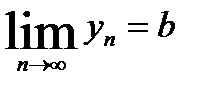читают так: предел последовательности у_n при стремлении n к бесконечности равен b.

На практике используется еще одно истолкование равенства 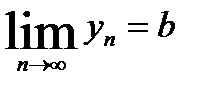, связанное с приближенными вычислениями: если последовательность у_n = f(_n) сходится к числу b, то выполняется приближенное равенство f(_n)≈b, причем это приближенное равенство тем точнее, чем больше n.

Необходимое условие сходимости произвольной числовой последовательности:

Для того чтобы последовательность сходилась, необходимо, чтобы она была ограниченной.

Достаточное условие сходимости последовательности.

Если последовательность монотонна и ограничена, то она сходится. (теорема К.Вейерштрасса)