Пределы функций. Нахождение пределов функции в точке и на бесконечности.

Теория пределов позволяет определить характер поведения функции у = f(x) при заданном изменении аргумента.

Пусть функция f(х) определена в некоторой окрестности точки х =х₀, за исключением, быть может, самой точки х₀.

Число А называется пределом функции f(х) в точке х₀, если для любого числа 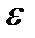>0 найдется такое положительное число 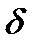, что для любого х 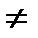х₀, удовлетворяющего неравенству | х - хо | < 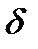, выполняется соотношение | f(x) - А | <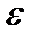

То, что функция f(x) в точке х₀ имеет предел, равный А, обозначают следующим образом:

Геометрически существование данного предела означает, что каково бы ни было 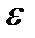>0, найдется такое число 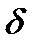, что для всех х, заключенных между х₀ + 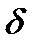, и х₀ - 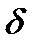(кроме, быть может, самой точки х_с), график функции у = f(x) лежит в полосе, ограниченной прямыми у = А + 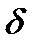и у = А- 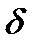(рис.1)

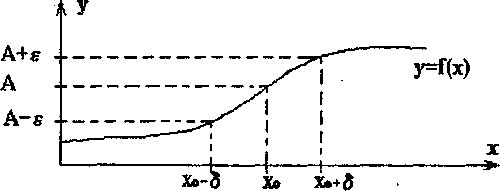
Рисунок 1

Таким образом, понятие предела функции дает возможность ответить на вопрос, к чему стремятся значения функции, когда значения аргумента стремятся к х₀

Число А называют пределом функции f(x) при х, стремящимся к х₀, если разность f(x) - А по абсолютной величине есть величина бесконечно малая.

Понятие бесконечно малой величины.

В природе существует много таких переменных величин, которые в процессе своего изменения неограниченно приближаются к нулю. Таким величинам присвоено специальное название -"бесконечно малые" величины.

Переменная величина х_п называется бесконечно малой, если она в процессе изменения становится и затем остается по абсолютной величине меньше любого, наперед заданного, сколько угодно малого положительного числа, т.е. х_п < 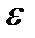( 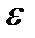- эпсилон). Рассмотрим колебание математического маятника.

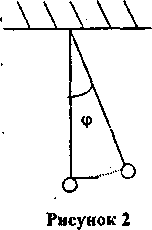
Математическим маятником называется материальная точка, подвешенная на тонкой, невесомой, нерастяжимой нити.

Пусть в начальный момент времени маятник отклонен от положения равновесия на угол 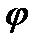= 15°. Если маятник отпустить, то он будет совершать колебания. Из-за сопротивления среды амплитуда колебания маятника будет постепенно уменьшаться; поэтому какое бы положительное число ни было задано, угол 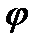по абсолютной величине станет и впредь будет оставаться меньше .

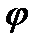Следовательно, угол в данном процессе является бесконечно малой величиной.

Примерами бесконечно малой величины являются: масса тающей в воде льдины, разность уровней однородной жидкости в сообщающихся сосудах и т.д.

Пусть задана числовая последовательность а_n,n 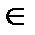N. Тогда последовательность S_n = а₁+ а₂+а₃+…+а_n = 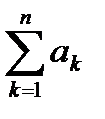, n N называется числовым рядом и обозначается а₁+ а₂+а₃+…+а_n + … или .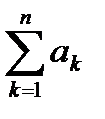

Числа а_1, а_{2, …}называется членами ряда 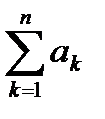, соответственно первым, вторым и т.д.; а_n называется n – м или общим членом ряда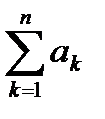

Ряд 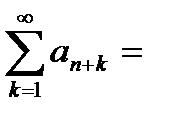а_n₊₁+ а_n+₂+ а_n+₃+… = 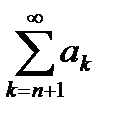называется n – _м остатком ряда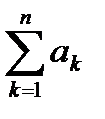

Согласно определению ряды – это особый вид последовательностей, поэтому можно говорить о сходимости и расходимости рядов.

Ряд называется сходящимся, если последовательность его частичных сумм сходится.

Если последовательность частичных сумм ряда расходится, то он называется расходящимся.

Ряд а₂+а₃+…+а_n + … или 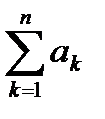.называется сходящимся, если существует предел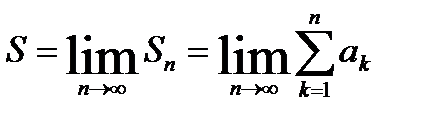

Этот предел называется суммой ряда а₂+а₃+…+а_n + … или .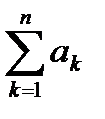

Если ряд а₂+а₃+…+а_n + … или 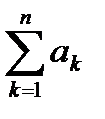сходится и Ы – его сумма, то будем писать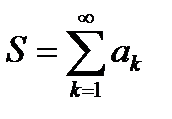

Теорема 1. Если ряд сходится, то и любой его остаток сходится. Если какой–нибудь остаток ряда сходится, то и ряд сходится.

Теорема 2. Если ряды с общими членами а_nи b_n сходятся и 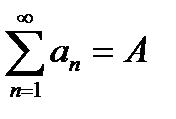, , 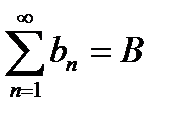то для любых чисел α и β ряд с общим членом с_n = αa_n и βb_n сходится и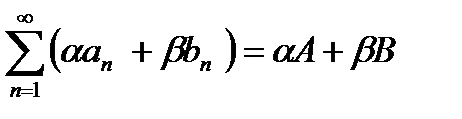

Пример:

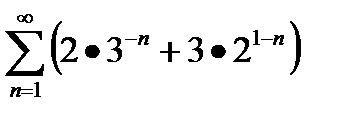
Решение:

Общий член этого ряда имеет вид

с_n =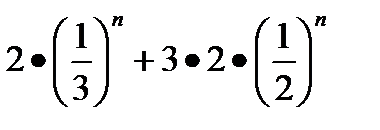

Ряды с общими членами а_{n = 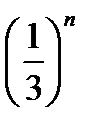и}b_n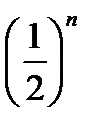₌сходятся и

,

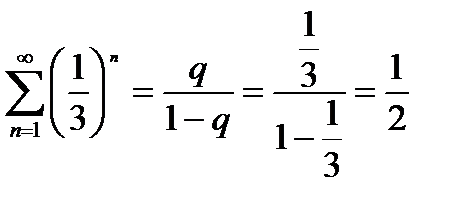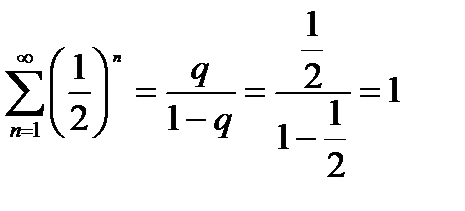
В силу теоремы 2 данный ряд сходится и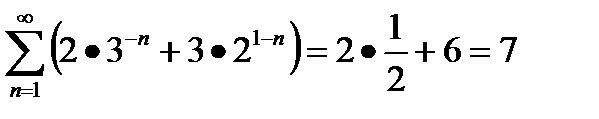

Теорема 3. (необходимое условие сходимости ряда)Если ряд с общим членом а_nсходится, то а_n 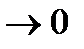при n .

<11 12 131415 16 17 >

Дата добавления: 2016-06-05; просмотров: 2369;