Понятие о дифференциальном уравнении

Определение. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.

Определение. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Дифференциальные уравнения широко применяются в области медицины: это волновые и колебательные движения, вязкость крови и т.д.

Определение. Решением дифференциального уравнения называется любая функция y = j(x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.

Интегральная кривая – это график решения дифференциального уравнения, т.е график функции, удовлетворяющей этому уравнению.

Общим решением дифференциального уравнения y∕ = j(x,у), в области определения D(f) называется функция y = j (x, С), обладающая следующими свойствами:

1. Она является решением данного уравнения при любых значениях произвольной постоянной С, принадлежащих некоторому множеству.

2. для любого начального условия у(х₀) = х₀ : (х_0, у₀) Є D (f) 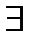! C = C₀, при котором решение y = j (x, С₀), удовлетворяет заданному условию.

Всякое решение y = j (x, С₀), получается из общего решения y = j (x, С) при конкретном значении С = С₀, называется частным решением дифференциального уравнения.

Пример 1: Найти частное решение дифференциального уравнения у^/ = 2у – 6, если х = 0, у = 4.

Решение:

dу = 2(у-3)dх

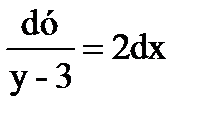
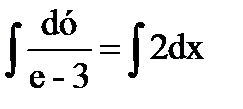общее решение

ln(у – 3) = 2х + С

ln(4 – 3) = 0 + С

C = ln 1 = 0

ln(у – 3) = 2х

2х = 2хlnе = lne^2x

у – 3 = lne^2x

у = lne^2x + 3 – частное решение.

Дифференциальные уравнения описывают многие примеры самых разных процессов природы. Например: поглощение света в растворе, фармакологическая кинетика.

Пример 1: Найдем закон Т(t) остывания кипящей воды до комнатной температуры (t_комн=20⁰) и время достижения 40⁰, если до 60⁰ вода остывает за 20 мин. Известно, что мгновенная скорость остывания линейно зависит от разницы Т и t_комн.

Решение:

Составим дифференциальное уравнение:

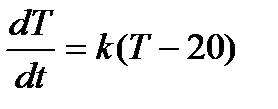
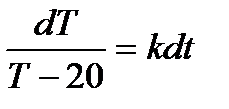
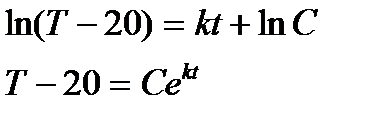
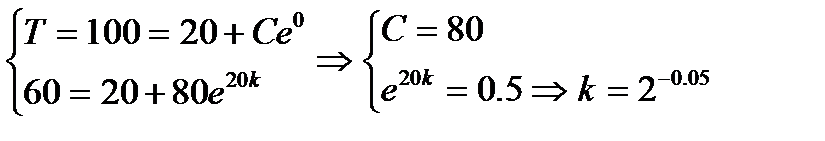
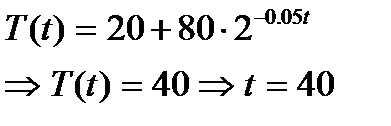
В медицинских приложениях дифференциальные уравнения используются для:

· определения скорости кровотока, скорости движения клапанов и стенок сердца (эхокардиография), определение вязкости крови и других параметров гемодинамики;

· описания медико- биологических приложений ультразвука: эхоэнцефалограмма, УЗИ, ультразвуковая физиотерапия, ультразвуковая локация и кардиография;

· описания процессов физиологической акустики, которая изучает устройство и работу звуковоспринимающих и звуковоспроизводящих органов человека и животных.