Правило нахождения общего решения.

Для нахождения общего решения дифференциального уравнения с разделяющимися переменными следует:

a). Разделить переменные, т.е. преобразовать данное уравнение к виду

р(у)dу = f(х)dх

b). Проинтегрировать обе части полученного уравнения по у и х соответственно, т.е. найти некоторую первообразную Р(у) функции р(у) и некоторую первообразную F(х)функции f(х)

c). Написать уравнение

Р(у) = F(х) + С, где С – произвольная постоянная.

Например:

Решить дифференциальное уравнение :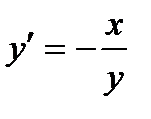

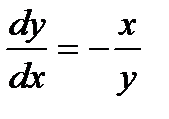
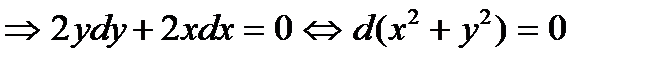интегрируя, получаем:

x² + y² = C = R² (рис.3)

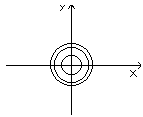рис.3

Полученное уравнение является уравнением окружности радиуса R с центром в точке (0;0). Оно при каждом фиксированном R>0 определяет две дифференцируемые функции

у = ±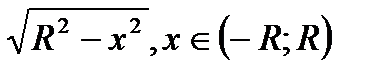

2) Однородные уравнения.

Под однородными уравнениями понимаются уравнения вида 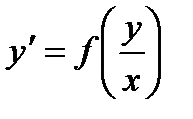. Для их решения требуется сделать замену 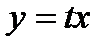, после чего получится уравнение с разделяющимися переменными: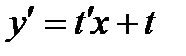

.

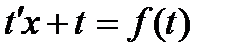
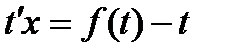
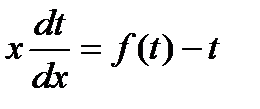
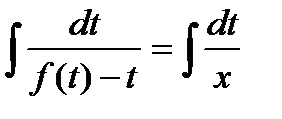Уравнения вида 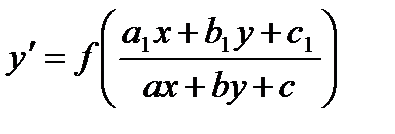. Такие уравнения сводятся к однородным заменой переменных. В случае, если прямые 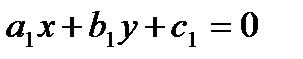и 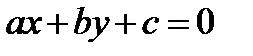пересекаются в точке 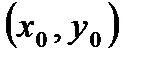, то замена 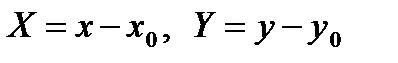приведет уравнение к однородному. Если же эти прямые не пересекаются, то 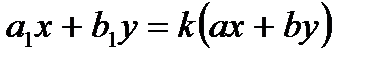и замена 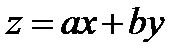приведет к уравнению с разделяющимися переменными.