Свойства определенного интеграла.
1. Определенный интеграл от суммы конечного числа функций fi(x), f2(x),... ,fn(x), заданных на отрезке [а, Ь], равен сумме определенных интегралов от слагаемых функций:
2. Постоянный множитель к подынтегральной функции можно выносить за знак определенного интеграла
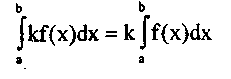
3. Если верхний и нижний пределы интегрирования поменять местами, то определенный интеграл сохранит абсолютную величину и изменит свой знак на противоположный:
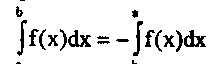
4. Если пределы интегрирования равны между собой, то определенный интеграл равен нулю:
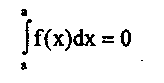
7. Связь между определенным и неопределенным интегралами. Формула Ньютона - Лейбница.
Общность обозначения определенного неопределенного интегралов подчеркивает тесную связь между ними, хотя определенный интеграл есть число, а неопределенный интеграл - совокупность первообразных функций. Связь между определенным и неопределенным интегралами устанавливает формула Ньютона - Лейбница.
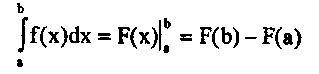
Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования. Вертикальная черта с верхним и нижним пределами, стоящая справа от символа функции F(x), называется знаком двойной подстановки.
Методы вычисления определенного интеграла:
1) метод подстановки или замены переменной 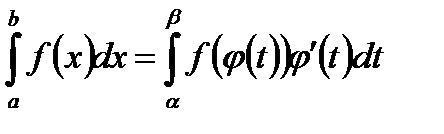
2) метод интегрирования по частям 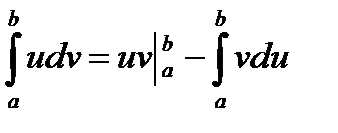
Дата добавления: 2016-06-05; просмотров: 2695;











