Понятие определенного интеграла.
Понятие определенного интеграла широко используется в математике и прикладных науках. С его помощью вычисляют площади, ограниченные кривыми, объемы тел произвольной формы и т.д. Рассмотрим задачу по определению площади криволинейной трапеции, приводящую к понятию определенного интеграла.
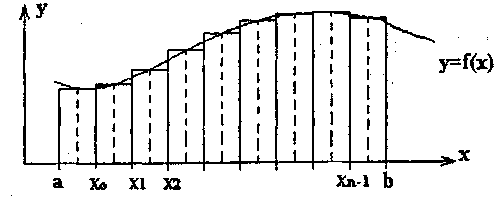
Фигура, ограниченная данной кривой у = f(x), отрезком [а,Ь] оси Ох и прямыми х = а и х = Ь, называется криволинейной трапецией
Предположим, что f(x) > 0 на отрезке [а,Ь], т.е. криволинейная трапеция расположена над осью Ох. Для вычисления площади S данной криволинейной трапеции разобьем отрезок [а,Ь] произвольным образом на п частей и обозначим точки деления:а = х0 <x1<x2<…<xn-1<xn = b Проведя из этих точек перпендикуляры до пересечения точек с кривой, получим значение функции в этих точках:
- 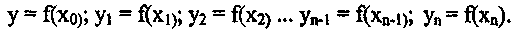
В результате площадь криволинейной трапеции окажется разбитой на сумму площадей элементарных криволинейных трапеций.
На отрезках Δхо, Δх1 ... , Δxn-1. возьмем произвольные точки Со, С1, С2, ... ,Cn-1 и проведем перпендикуляры из этих точек до пересечения с кривой у = f(x). Получим f(co), f(c1), f(с2),..., f(сn-1)
Далее постоим ступенчатую фигуру, состоящую из прямоугольников, имеющим основанием отрезки Δхо, Δх1 ... , Δxn-1, высотой –ординаты f(co), f(c1), f(с2),..., f(сn-1) Эта фигура ограничена ломаной линией. Площадь Sn полученной ступенчатой фигуры зависит от числа п и длины отрезков Δxi(i = О, 1, 2 ,..., п-1). При неограниченном увеличении числа п и уменьшении отрезка Δхi ломанная, ограничивающая ступенчатую фигуру, будет приближаться к площади трапеции S. Отсюда ясно, что площадью криволинейной трапеции, ограниченной линией у = f(х), следует называть предел, к которому стремиться переменная площадь Sn ступенчатой фигуры, ограниченной ломаной линией, при стремлении к нулю длины отрезка Δxi(i = О, 1, 2 ,..., п-1). Площадь Sn равна сумме площадей прямоугольников, построенных на отрезках:
Sn= f(c0)Δx0 + f(c1)Δx1 + …+f(cn-1)Δxn-1
Если теперь неограниченно увеличивая п частей разбиения так, чтобы длина отрезков Δxi(i = О, 1, 2 ,..., п-1) стремилась к нулю, то площадь криволинейной трапеции будет равна пределу суммы, каждое слагаемое которой равно произведению значения функции в точке отрезка f(ci) на величину этого отрезка Δхi;
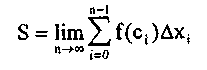
Если существует конечный предел этой интегральной суммы, то этот предел называется определенным интегралом от функции f(x) на отрезке [а, Ь] и обозначают:
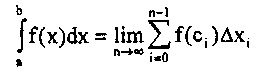
(читается «определенный интеграл от а до b от икс дэ икс»).
При этом f(x) называется подынтегральной функцией, х переменной интегрирования, числа а и b - соответственно нижним и
верхним пределом интегрирования.
Определенный интеграл есть число, его значение зависит от вида функции f(x) и значений верхнего и нижнего пределов. На основании выше изложенных формул можно записать: площадь криволинейной трапеции численно равна интегралу от функции, ограничивающей трапецию, взятому по основанию [а, Ь]:
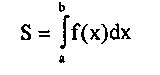
Дата добавления: 2016-06-05; просмотров: 2694;











