Определение функции нескольких переменных.

Частные функции.

Цели: создание благоприятных условий для изучения производной при исследовании и построении графиков функций; ввести понятие функции нескольких переменных.

I. Вопросы для повторения

1) Что называется функцией y=f(x)?

2) Какая функция называется возрастающей на промежутке?

3) Какая функция называется убывающей на промежутке?

4) Какая функция называется монотонной на промежутке?

II. Текст для чтения

С помощью производной можно определить монотонность функции на любом промежутке области определения.

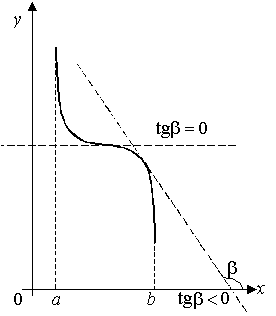Рисунок 12

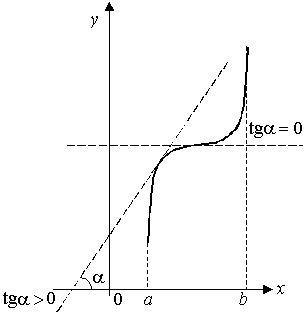Рисунок 13

Функция y=f(x) (Рисунок 13) возрастает на промежутке (a; b). Касательная в любой точке функции y=f(x) образует с положительным направлением оси Ox острый угол или угол, равный 0. Значит, 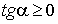. Но .

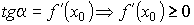Производная функции y=f(x) в каждой точке (a; b) неотрицательна.

Необходимое условие возрастания функции:

Если функции y=f(x) возрастает на (a; b), то 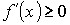для всех x, принадлежат (a; b).

Пример: Функция 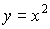возрастает на 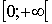, т.к. .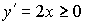

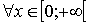Функция 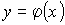(Рисунок 12) убывает на (a; b)

Касательная в любой точке графика функции 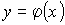образует с положительным направлением оси Ox или тупой угол, или угол, равный нулю. Значит, tg .

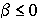Но 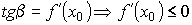.3

Необходимое условие убывания функции:

Если функция y=f(x) убывает на ]a; b[, то 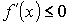для всех x, принадлежащих (a; b).

Пример: функция 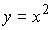убывает на (- 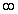;0 ], так как ее производная на этом промежутке отрицательна.

Справедливы и обратные теоремы.

Теорема (достаточное условие возрастания функции):

Если f'(x)>0 для всех x, принадлежащих (a;b), то функция y=f(x) возрастает на (a ; b)

Теорема (достаточное условие убывания функции):

Если f'(x)<0 для всех x, принадлежащих (a;b), то функция y=f(x) убывает на (a; b)

Значит, чтобы найти промежутки монотонности, нужно:

1)найти область определения функции y=f(x),

2)вычислить производную функции f'(x),

3)решить уравнение f'(x)=0

4)отметить на числовой прямой область определения функции и критические точки;

3)определить знак производной f'(x) на каждом промежутке.

Задача 1.Найти промежутки монотонности функции

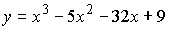
1.D(x)=R

2.

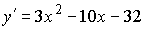
3.Решить неравенства 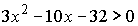и 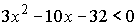методом интервалов.

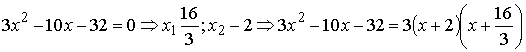
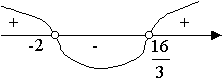Ответ: функция y=f(x) возрастает на 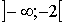и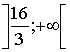

убывает на .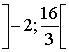

Задача 2. Найти промежутки возрастания и убывания функции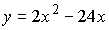

Упражнения

Найти промежутки монотонности функций:

1)

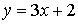
2)

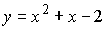
3)

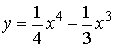
4)

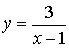
5)

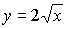
ТОЧКИ ЭКСТРЕМУМА

Определение: Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими.

Теорема Ферма (необходимое условие существования функции):

Если функция имеет производную в каждой точке промежутка (a ;b) и 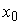- точка экстремума, то в этой точке производная равна нулю .

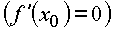На основании теоремы Ферма можно сделать вывод: функция может иметь экстремум только в критических точках. Но обратное утверждение верно не всегда.

Теорема: (достаточное условие существования экстремума):

Пусть функция y=f(x) определена, непрерывна и дифференцируема на (a;b) и 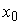- это критическая точка.

Тогда:

1) если при переходе через точку 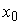производная функции изменяет свой знак с ''-'' на ''+'', то точка 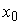-это точка минимума.

2) если при переходе через точку 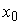производная функции изменяет свой знак с ''+'' на ''-'', то точка 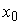- это точка максимума.

Значит, чтобы найти точки экстремума функции y=f(x) на (a; b) нужно:

1) Найти .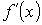

2) Найти критические точки функции y=f(x).

3) Определить знак 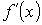на каждом из промежутков, на которые разделили промежуток (a; b) критические точки.

4) С помощью теоремы, выражающей достаточное условие существования экстремума, найти точки максимума и минимума.

Задача. Найти точки экстремума функции 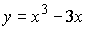на [-3;3]

1)

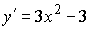
2)

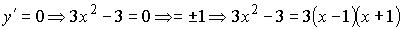
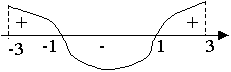
3)

4)

x		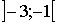-1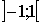
	+		+		-
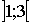
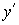
				-2
	max		min

Ответ: точка максимума (-1;2), точка минимума (1;-2)

Упражнения

Найти экстремумы функции:

1)

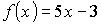
2)

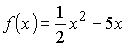
3)

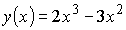
Контрольные вопросы:

1.Необходимое условие возрастания функции на промежутке (a ;b).

2.Необходимое условие убывания функции на промежутке (a ;b).

3.Достаточное условие возрастания функции на промежутке. (a ;b).

4.Достаточное условие убывания функции на промежутке (a ;b).

5.Закончить текст:

а) если 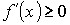для всех x 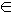(a;b),то . . .

б) если . . . , то функция y=f(x) убывает на этом промежутке.

6.Найти промежутки монотонности функции по ее графику

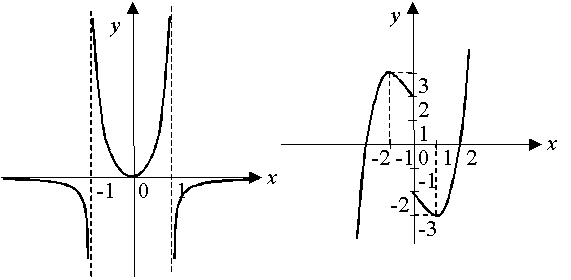
7.В каких точках области определения дифференцируемой функции ее монотонность изменяется: возрастание изменяется на убывание и наоборот?

8.Какие точки называются критическими?

9.Необходимое условие существования экстремума функции.

10. Достаточное условие существования экстремума функции.

11. Какая точка называется внутренней?

12. Какие точки называется точками экстремума?

13. Какая точка называется точкой максимума?

14. Какая точка называется точкой минимума?

Домашнее задание

Заполните в рабочей тетради занятие 3

Лекция № 3

Тема: Интегральное исчисление. Последовательности пределы и ряды