ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ

Есть функция y=f(z), где .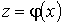

Функция, заданная формулой 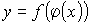, называется сложной функцией.

Пример: функция 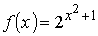- сложная

Производную сложной функции 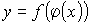можно найти по формуле: .

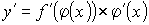Задача 1.Найти производную функции .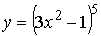

Решение:

Пусть 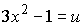, тогда .

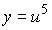По теореме о производной сложной функции.

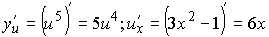
Тогда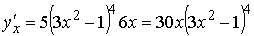

Упражнения Найти производную функции: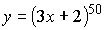

Производные элементарных функций:

1. (uⁿ)' = nu^n-

2. (a^u)' = a^u lna u'.

3. (e^u)' = e^u u'.

4. (log_a u)' = u'/(u ln a).

5. (ln u)' = u'/u.

6. (sin u)' = cos u u'.

7. (cos u)' = - sin u u'.

8. (tg u)' = 1/ cos²u u'.

9. (ctg u)' = - u' / sin²u.

10. (arcsin u)' = u' / .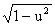

11. (arccos u)' = - u' / .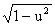

12. (arctg u)' = u'/(1 + u²).

13. (arcctg u)' = - u'/(1 + u²).

Контрольные вопросы

Что такое приращение аргумента и приращение функции?

В чем состоит геометрический смысл производной?

В чем состоит механический смысл производной?

Сформулируйте определение функции в точке?

Как называется процесс нахождения производных функций?

Сформулируйте правила вычисления производных?

Чему равна производная функции f(х) = хⁿ?

Чему равна производная сложной функции?

Домашнее задание

Заполните в рабочей тетради занятие 1, 2

Лекция № 2

Тема: Дифференциальное исчисление