Формула Ньютона-Лейбница.
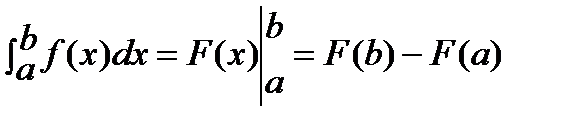 ,
,
где F(x)-одна из первообразных f(x).
Рассмотрим 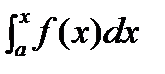 , он является одной из первообразных f(x), т.е.
, он является одной из первообразных f(x), т.е. 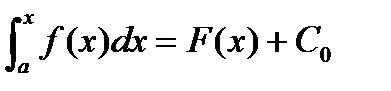
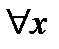 , где C0 – конкретное значение const. Найдем C0. Подставим вместо верхнего предела x=aÞ
, где C0 – конкретное значение const. Найдем C0. Подставим вместо верхнего предела x=aÞ 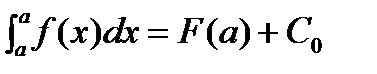 ÞC0=-F(a)Þ
ÞC0=-F(a)Þ 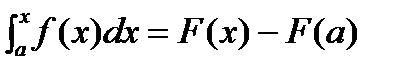 . Подставим вместо верхнего предела x=bÞ
. Подставим вместо верхнего предела x=bÞ 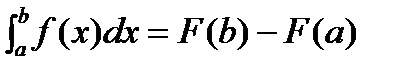
Формула позволяет вычислять определенный интеграл.
Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции. Только с открытием этой формулы определенный интеграл смог получить то значение в математике, какое он имеет в настоящее время. Хотя с процессом, аналогичным вычислению определенного интеграла как предела интегральной суммы, были знакомы еще в древности (Архимед), однако приложения этого метода ограничивались теми простейшими случаями, когда предел интегральной суммы мог быть вычислен непосредственно. Формула Ньютона-Лейбница значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различных задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла к технике, механике, астрономии и т.д.
Пример:
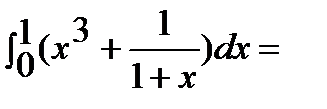
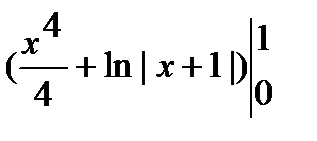
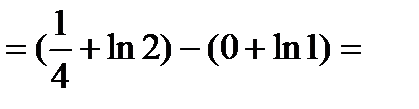
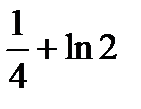 .
.
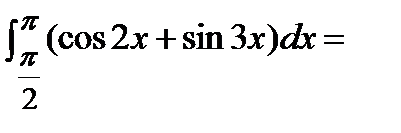
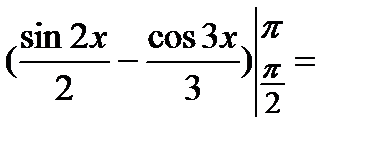
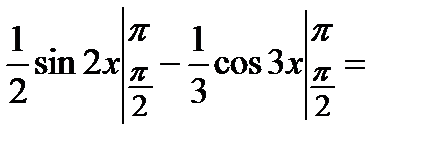
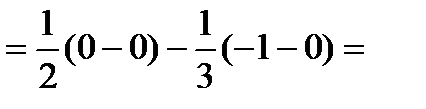
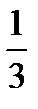 .
.
Дата добавления: 2016-06-05; просмотров: 1747;











