Несобственные интегралы первого рода (по бесконечному промежутку).
Определение: Пусть функция 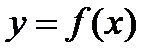 непрерывна на промежутке
непрерывна на промежутке 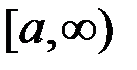 , тогда очевидно, что при любом
, тогда очевидно, что при любом 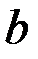 имеет смысл интеграл
имеет смысл интеграл 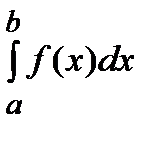 . Будем расширять промежуток
. Будем расширять промежуток 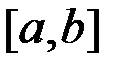 , увеличивая
, увеличивая 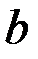 . Тогда, если существует предел:
. Тогда, если существует предел:
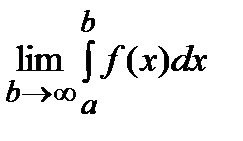 , то этот предел называется несобственным интегралом от функции
, то этот предел называется несобственным интегралом от функции 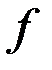 по бесконечному промежутку
по бесконечному промежутку 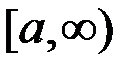 и обозначается
и обозначается 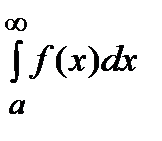 .
.
Отметим, что если указанный предел существует и конечен, то интеграл 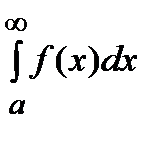 называется сходящимся (говорят, что он сходится). В противном случае (если предел бесконечен или не существует) говорят, что
называется сходящимся (говорят, что он сходится). В противном случае (если предел бесконечен или не существует) говорят, что 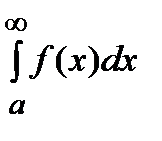 расходится.
расходится.
Аналогично вводится понятие несобственного интеграла 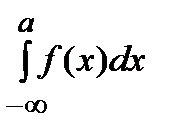 по промежутку
по промежутку 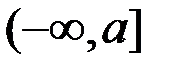 .
.
Определение: Несобственный интеграл 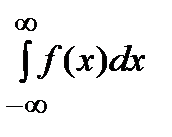 определяется как следующая сумма несобственных интегралов:
определяется как следующая сумма несобственных интегралов:
 =
= 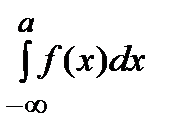 +
+ 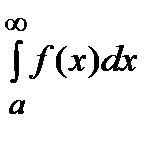 .
.
Отметим, что легко показать, что так определенный интеграл 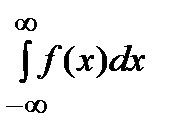 не зависит от выбора точки
не зависит от выбора точки 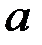 . Этот интеграл называется сходящимся, если сходящимися являются интегралы
. Этот интеграл называется сходящимся, если сходящимися являются интегралы 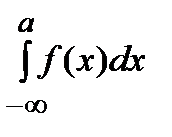 и
и 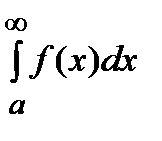 , в противном случае он называется расходящимся.
, в противном случае он называется расходящимся.
Примеры:
1. Вычислить несобственный интеграл или доказать его расходимость:
а) 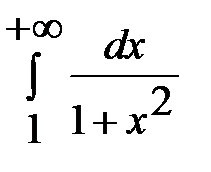 =
= 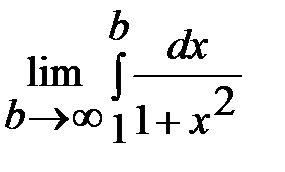 =
= 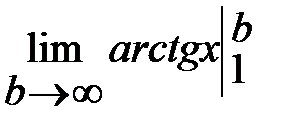 =
= 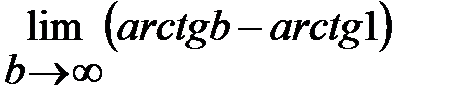 =
=
= 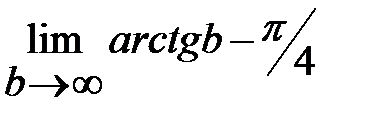 =
= 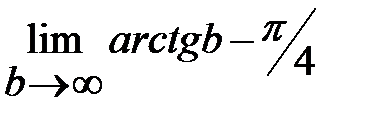 =
= 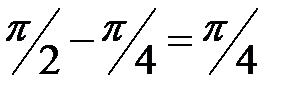
б) 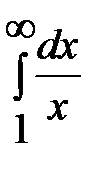 =
= 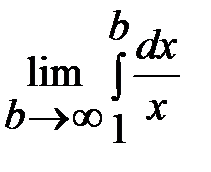 =
= 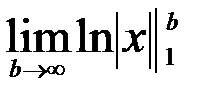 =
= 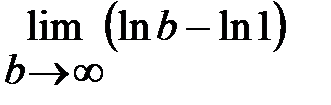 =
=  (интеграл расходится)
(интеграл расходится)
в) 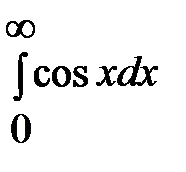 =
= 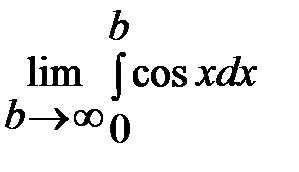 =
= 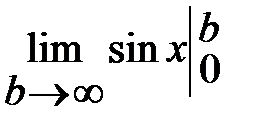 =
= 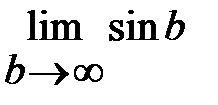 Поскольку последний предел не существует, то интеграл расходится.
Поскольку последний предел не существует, то интеграл расходится.
Дата добавления: 2016-06-05; просмотров: 2384;











