Интегрирование по частям и замена переменной в определенном интеграле.
Интегрирование по частям.
Пусть u и v – дифференцируемые функции от х.
Тогда 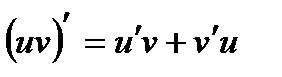 . Интегрируя обе части тождества в пределах от а до в, получим:
. Интегрируя обе части тождества в пределах от а до в, получим:
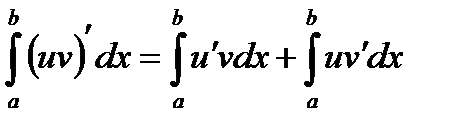 . (1)
. (1)
Так как 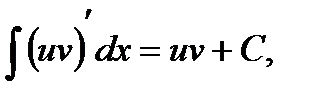 то
то 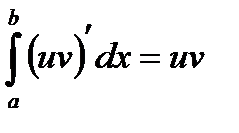 │
│ 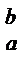 ; поэтому равенство (1) может быть записано в виде: uv│
; поэтому равенство (1) может быть записано в виде: uv│ 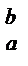 =
= 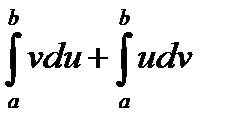 , или окончательно
, или окончательно
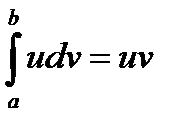 │
│ 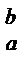 -
- 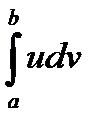 .
.
Пример: 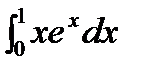 =
= 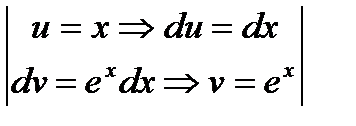 =
= 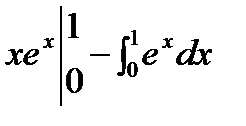 =1.
=1.
Интегрирование с заменой переменной.
Теорема.
Пусть дан интеграл 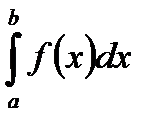 , где функция f(x) непрерывна на [a,b]. Введем новое переменное формуле x=
, где функция f(x) непрерывна на [a,b]. Введем новое переменное формуле x= 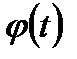 .
.
Если 1) 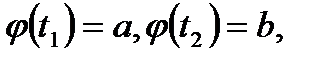
2) 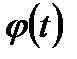 и
и 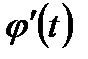 непрерывны на отрезке [t1,t2],
непрерывны на отрезке [t1,t2],
3) 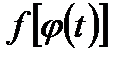 определена и непрерывна на отрезке [t1,t2], то
определена и непрерывна на отрезке [t1,t2], то 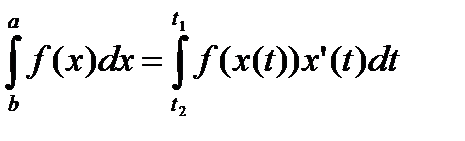 , где
, где 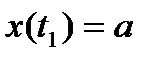 ,
, 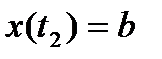 . (1)
. (1)
Доказательство:
Если F(x) есть первообразная для функции f(x),то можем написать следующие равенства:
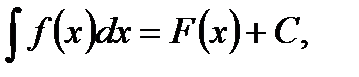 (2)
(2)
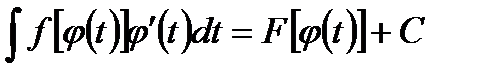 (3)
(3)
Справедливость последнего равенства проверяется дифференцированием обеих частей по t. Из равенства (2) получаем:
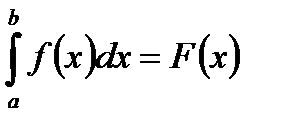 │
│ 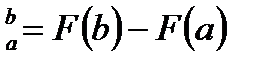 .
.
Из равенства (3) получаем:
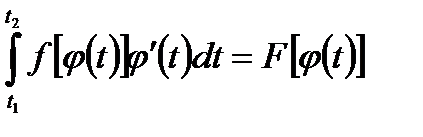 │
│ 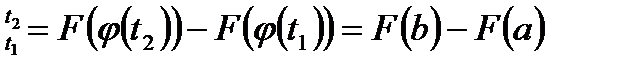 .
.
Правые части последних выражений равны, следовательно, равны и левые.
Теорема доказана.
Замечание: При замене переменной в определённом интеграле нужно поменять пределы интегрирования, возвращаться к старой переменной нет необходимости.
Пример:
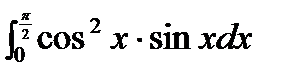 =
= 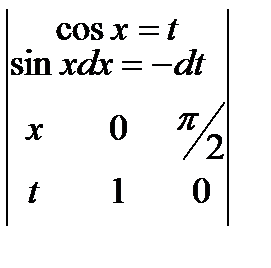 =
= 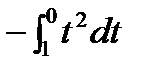 =
= 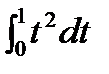 =
= 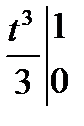 =
= 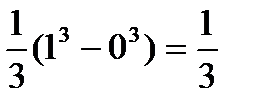 .
.
Дата добавления: 2016-06-05; просмотров: 1797;











