Полярная система координат.
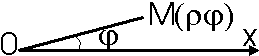 Рассмотрим на плоскости точкуО, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью.
Рассмотрим на плоскости точкуО, которую называют полюсом, и луч, выходящий из этой точки, который называется полярной осью.
Зададим на полярной оси масштаб. Каждой точке M поставим в соответствие два числа r - длина радиус-вектора 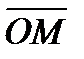 и j - угол между радиус-вектором точки M и положительным направлением полярной оси.
и j - угол между радиус-вектором точки M и положительным направлением полярной оси.
Таким образом, любая точка в полярной системе координат будет иметь две координаты M(r,j), r – полярный радиус, j – полярный угол. Очевидно, что r – величина неотрицательная (как длина любого вектора), а угол может выбираться по договоренности (для однозначности определения координат) из промежутков 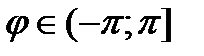 или
или 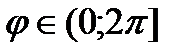 .
.
Если угол j откладывается от полярной оси против хода часовой стрелки, то его будем считать положительным, если по часовой стрелке, то отрицательным.
Изображение линий в полярной системе координат.
r= R – окружность с центром в полюсе и радиусом R.
j= a - луч под углом 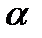 к полярной оси.
к полярной оси.
r= j – при построении любой кривой в полярной системе координат, нужно задавать различные значения полярного угла j и вычислять соответственно значения полярного радиуса r. Если r получится меньше нуля, то картинки не будет (этой части рисунка не будет)
| Спираль Архимеда | Кардиоида | 3-х лепестковая роза | Лемниската Бернулли | |
| r=j | r=1+cosj | r=cos3j | r=4cosj | r2=cos2j |
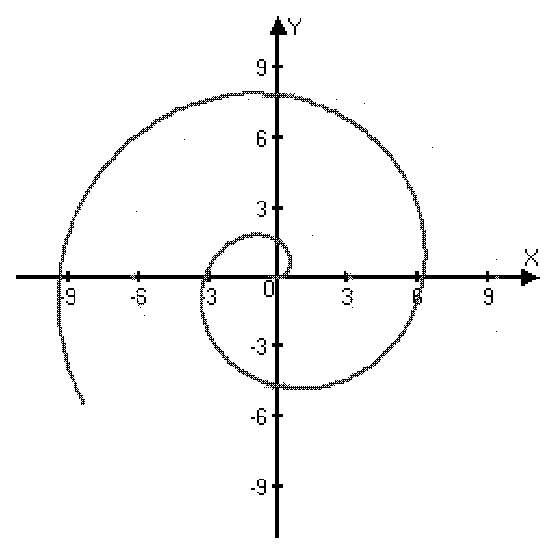
| 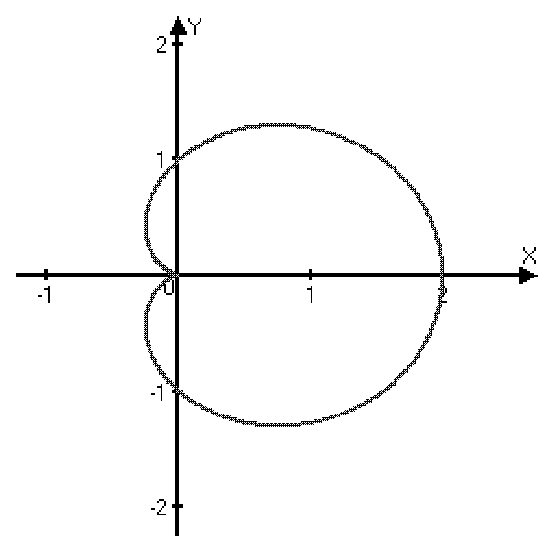
| 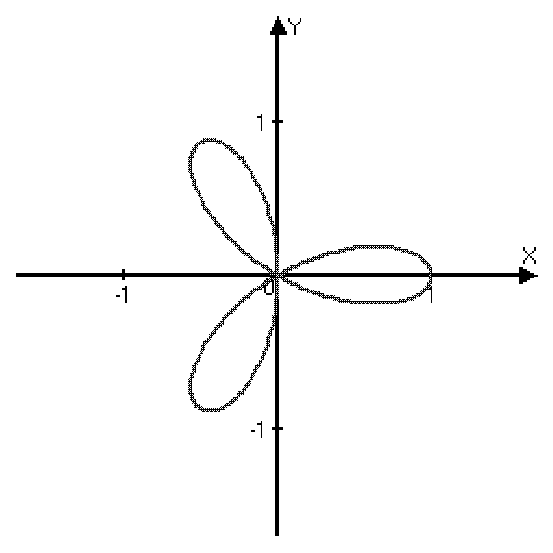
| 
| 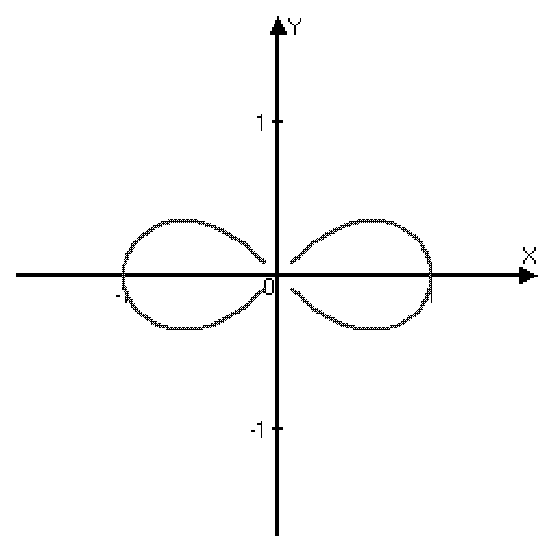
|
Связь между декартовой и полярной системами координат.
Если полярную и декартову систему координат совместить так, чтобы полюс совпал с началом координат, а полярная ось с положительным направлением оси 0x, то можно получить формулы перехода от полярных координат (r;j ) к декартовым (x;y):
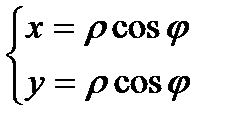 , и от декартовых к полярным:
, и от декартовых к полярным: 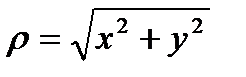 ,
, 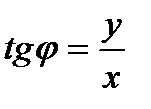
Дата добавления: 2016-06-05; просмотров: 1944;











