Вычисление длины дуги кривой в декартовой системе координат.

Нужно вычислить длину плоской кривой L, заданной уравнением y=f(x) на отрезке [a,b].

Разобьем отрезок на части точкамиx_i где i=0…n, a=x₀<x₁<x₂<…<x_n=b.

Через эти точки проведем прямые параллельные оси OY, которые разобьют кривую на n частей. Впишем в эти части ломаную.

Длина i-ого звена ломаной: Dl_i= .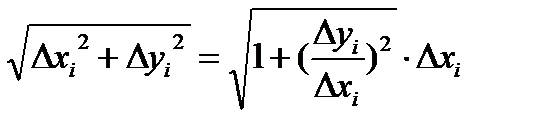

Просуммируем 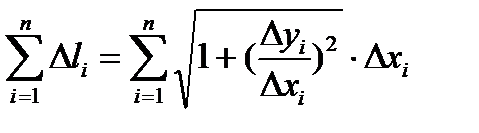, сумма длин звеньев ломаной приближенно равна длине кривой. Переходя к пределу, получим: = = .

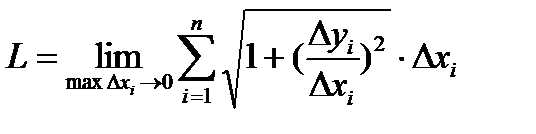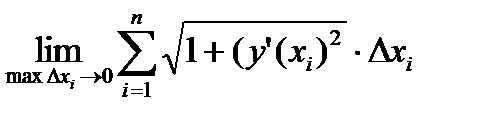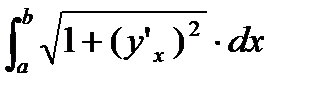
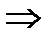
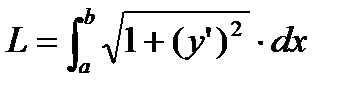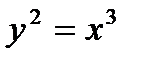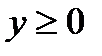Пример: Вычислить длину полукубической параболы , где , x=0, x=1.

; .

.

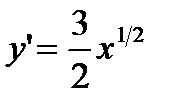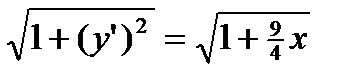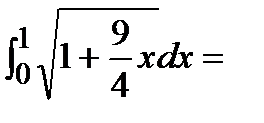
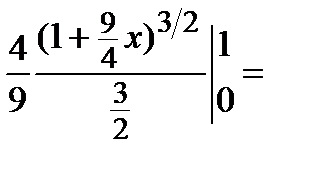
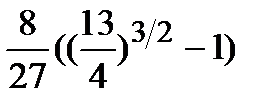Вычисление длины дуги кривой, заданной параметрически.

В декартовой системе координат длина дуги L= .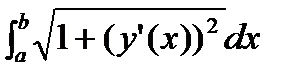

Предположим теперь, что кривая задана параметрически:

, , = .

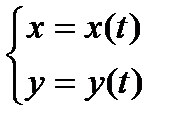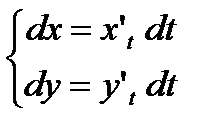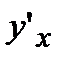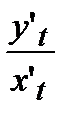Длина кривой заданной параметрически, выражается через определенный интеграл

L= .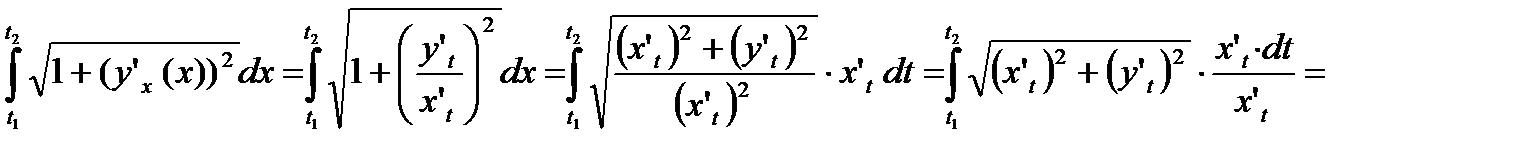

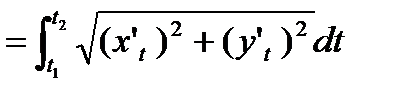Замечание: При вычислении длины кривой заданной параметрически нижний предел интегрирования должен быть меньше верхнего предела интегрирования.

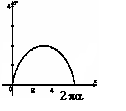Пример: Найти длину 1 арки циклоиды.

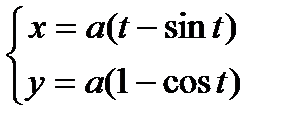
Вычислим длину 1 арки циклоиды

0£t£2p

= = = = = = =

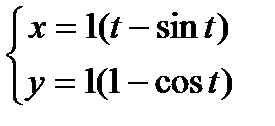
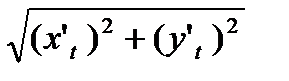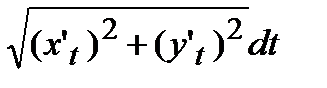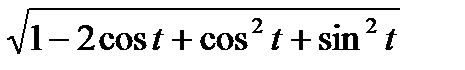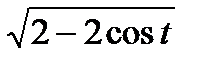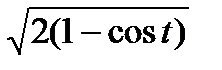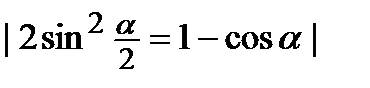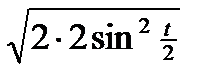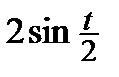
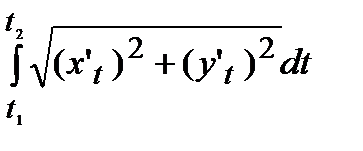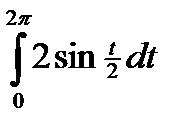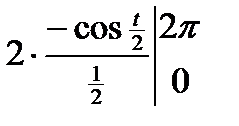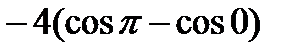L= = = = =-4(-1-1)=8.