Первообразная и неопределенный интеграл.
Определение: Первообразной F(x) для функции f(x) на промежутке 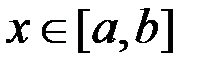 называют функцию, производная которой
называют функцию, производная которой 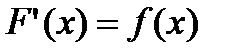 .
.
Пример. Для функции 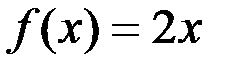 : первообразная
: первообразная 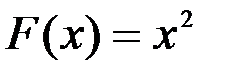 на R, так к
на R, так к 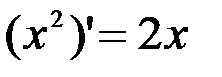 при любом х.
при любом х.
Лемма.Если производная функции на промежутке 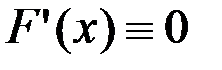 , то
, то 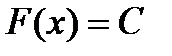 .
.
Доказательство: По теореме Лагранжа для любых x1, x2 Î выполняется 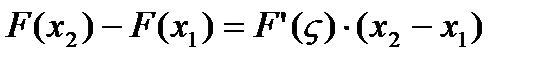 , где
, где 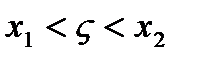 , так как
, так как 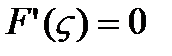 Þ
Þ 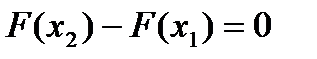 Þ
Þ 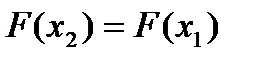 Þв силу произвольности точек x1 и x2 F(x) = C(const).
Þв силу произвольности точек x1 и x2 F(x) = C(const).
Ч.т.д.
Теорема: Пусть функция F(x) – первообразная f(x), Ф(x) – другая первообразная f(x) Þ F(x)=Ф(x)+С.
Доказательство: так как 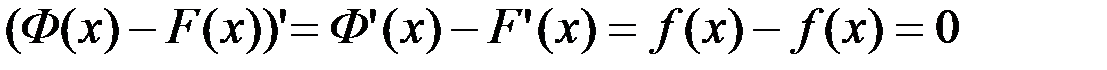 Þ по Лемме
Þ по Лемме 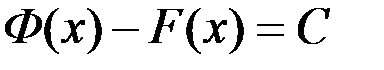 Þ
Þ 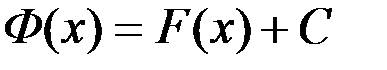 .
.
Ч.т.д.
Таким образом, из теоремы следует, что выражение 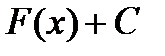 описывает все множество первообразных функции f(x).
описывает все множество первообразных функции f(x).
Определение: Неопределенным интегралом функции f(x) по переменной x называется множество всех её первообразных 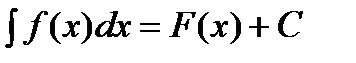 , где
, где 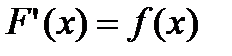 .
.
ò ‒ знак интеграла, f(x) – подынтегральная функция, x – переменная интеграла, 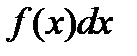 ‒ подынтегральное выражение, С – const интегрированная.
‒ подынтегральное выражение, С – const интегрированная.
Вычисление неопределенного интеграла называют интегрированием. Проверить правильность вычисления неопределенного интеграла можно продифференцировав результат.
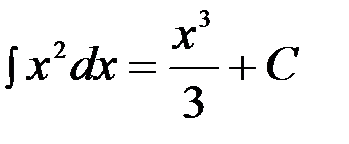 ;
; 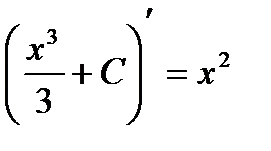 - верно.
- верно.
Свойства неопределенного интеграла.
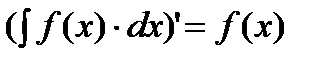
| |
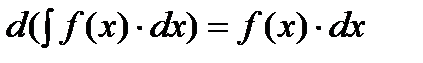
| |
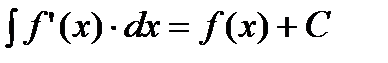
| |
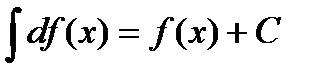
| |
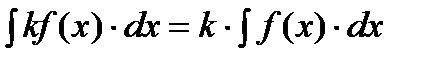
| |
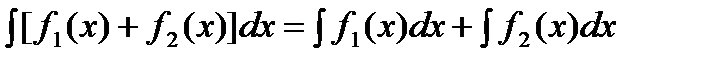
| |
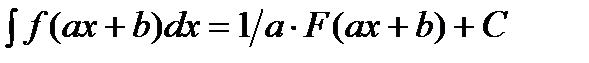
|
Дата добавления: 2016-06-05; просмотров: 1409;











