Несобственный интеграл.

Если криволинейная трапеция бесконечно вытянута вправо или вверх, то может быть конечная площадь. Примеры:

Пример. 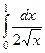= = 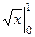1.

Но ведь область значений E(f) не является ограниченной. При вычислении мы даже и не заметили, что функция неограниченная в окрестности точки 0, т.е. 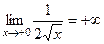. Так как первообразная ограниченная, и в неё можно просто подставить и 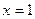. Вот график этой функции :

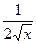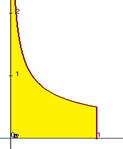
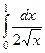можно рассматривать как предел .

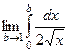Пример. Вычислить .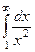

Решение. Такой интеграл можно рассматривать как предел интегралов вида 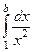при 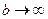. Если вычислить 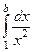то получится 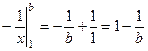. Предел .

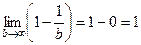Несмотря на неграниченность трапеции под интегралом, площадь конечна. Здесь область определения D(f) не является ограниченной. Тем не менее, трапеция слишком узкая, т.е. её ширина убывает достаточно быстро, чтобы площадь не превысила некоторое число. Так может быть, к примеру, если площади криволинейных трапеций между соседними целыми абсциссами убывают со скоростью сходящейся геометрической прогрессии.

Определение. Если функция 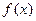определена и непрерывна на 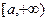, то предел 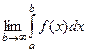называется несобственным интегралом 1-го рода от функции 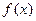, и обозначается .

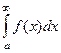Аналогично с помощью предела можно определить и несобственный интеграл 2 рода. Так, если функция имеет бесконечный предел на правой границе b то надо отступить на некоторое расстояние 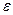и посчитать конечный интеграл, а затем перейти к пределу.

Определение. Если функция 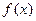определена и непрерывна на 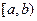и при этом предел 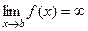, то 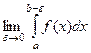называется несобственным интегралом 2-го рода от функции 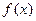, и обозначается .

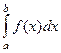Итак, если неограниченная D(f), то интеграл называется несобственным интегралом 1-го рода, а если E(f) то несобственным интегралом 2-го рода.

Если предел существует и является конечным числом, то несобственный интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется расходящимся.

Кстати, для сравнения, геометрическая прогрессия также бывает сходящейся либо расходящейся. Если площадь такой бесконечно вытянутой криволинейной трапеции разбить на части по целым числам, например от 1 до 2, от 2 до 3 и так далее, то если они образуют сходящуюся прогрессию, и в сумме равны некоторой константе, то интеграл сходится.

Примеры расходящихся несобственных интегралов.

Пример. 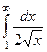= = 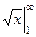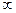. Здесь расходимость из-за неограниченности первообразной.

Пример. 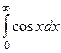= = 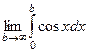= = 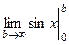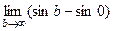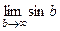. Но этот предел не существует, синус колеблется от -1 до 1 и при увеличении переменной его график не стремится ни к какой конкретной высоте. И хотя даже функция ограничена, несобственный интеграл расходится. Площадь криволинейной трапеции, при увеличении , то растёт, то снова убывает.

Пример = = = = = .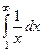

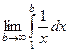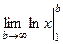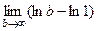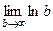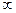Примеры сходящихся несобственных интегралов.

Пример. = = .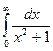

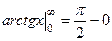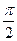Пример. = = .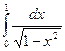

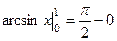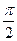Теорема 1. Несобственный интеграл 1-го рода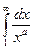

сходится тогда и только тогда, когда ,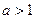

несобственный интеграл 2-го рода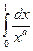

сходится тогда и только тогда, когда .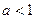

Доказательство. Сначала рассмотрим первообразную.

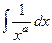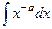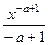= = , что можно записать в виде .

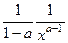Если пределы интегрирования от 1 до 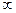, то не бесконечный результат получится лишь в том случае, когда переменная в знаменателе, то есть степень 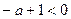, то есть 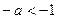, то есть .

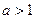А если пределы интегрирования от 0 до 1, то наоборот, наличие переменной в знаменателе приводит к тому, сто предел бесконечен, интеграл расходится. То есть для сходимости, надо чтобы степень была такая, чтобы переменная находилась именно в числителе. Тогда 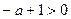, то есть, 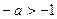, 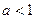. Что и требовалось доказать.

Обратите внимание, что в случае 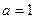расходятся оба этих интеграла, так как первообразная -это логарифм, а он не ограничен ни при 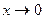, ни при .

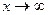Для таких интегралов 2 рода, для сходимости надо, чтобы степень перешла в положительные, например, если у функции степень 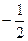, а у первообразной на 1 больше, уже 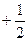. Если же она 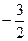, то после интегрирования станет 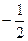, то есть ещё не переходит через 0 в положительные.

Примеры

1 рода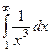
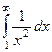
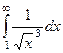
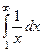
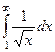
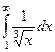
2 рода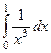
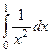
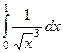
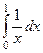
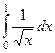
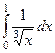
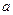
			1,5		1/2	1/3

Жёлтым цветом здесь выделены сходящиеся интегралы.

Теорема 2. Несобственный интеграл сходится 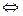первообразная на границах интегрирования имеет конечный предел.

Идея доказательства. Действительно, 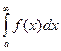= = 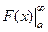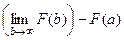. Второе слагаемое конечное число. Первое слагаемое (предел) есть конечное число тогда и только тогда, когда разность - конечное число. То есть, сходятся именно те несобственные интегралы, где график первообразной стабилизируется по высоте, т.е. имеет конечный предел 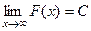. Если интеграл 1 рода, то 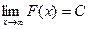равносильно сходимости.

Следствие (необходимый признак сходимости).

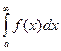сходится .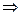

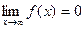Действительно, если 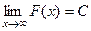то = = .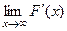

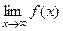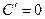Замечание. Это необходимый, а не достаточный признак, то есть, из сходимости следует, что f стремится к 0, но не наоборот. То есть, при 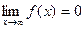могут быть как сходящиеся, так и расходящиеся интегралы, а вот если 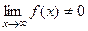, тогда только расходящиеся.

Рассмотрим 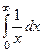и 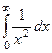. Здесь в обоих случаях 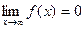выполнено. А тем не менее, первых из них расходится, а второй сходится. Их графики кажутся похожими, но ведь второй уменьшается существенно быстрее: так, при 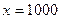значение у первой их них 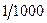, а у второй 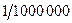, то есть в 1000 раз меньше! То есть кроме условия 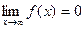важна ещё и скорость сходимости. Но если это условие не выполнено, то сходимости точно нет, в этом и состоит понятие «необходимый» признак.

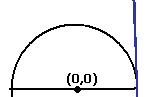
Как мы увидели, овольно нередкой является ситуация, когда производная стремится к бесконечности, а сама функция (то есть её первообразная) в той же точке является конечной. Геометрическая интерпретация. Рассмотрим верхнюю полуокружность. При приближении к точке (1,0) касательная стремится к вертикальному положению, тангенс угла её наклона к 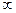. А при этом сама полуокружность 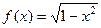ограничена по высоте:

Теорема 3. Пусть 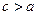. Несобственный интеграл 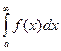сходится тогда и только тогда, когда сходится .

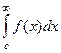Идея доказательства. Вся площадь равна 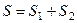. При этом 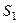заведомо является конечной, в этом случае число 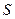конечно тогда и только тогда, когда 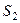конечно. Чертёж:

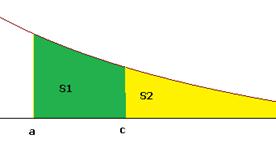
Теорема 4. Признак сравнения в конечной (непредельной) форме.

Если 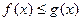и сходится 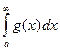, то сходится .

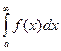Действительно, если интеграл для большей функции равен C, то для меньшей он меньше чем C, то есть, не равен бесконечности.

Пример.Выяснить сходимость интеграла .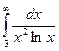

Учитывая тот факт, что при 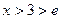верно 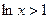, получается

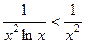. Тогда 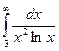< 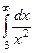, а он сходится, так как степень знаменателя больше 1. Тогда и исходный интеграл сходится.

Замечание. Аналогично тому, как мы ограничиваем сверху какой-либо сходящейся функцией, можно ограничить снизу какой-либо расходящейся функцией. Если интеграл от этой меньшей функции расходится, то и исходный тоже расходится.

Теорема 5. Признак сравнения в предельной форме.

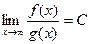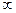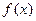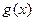Если , причём C отлично от 0 и от (то есть и бесконечно малые одного порядка). Тогда:

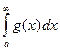сходится тогда и только тогда, когда 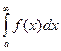сходится.

Пример на признак в предельной форме.

Выяснить сходимость интеграла .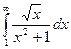

Рассмотрим для функции 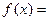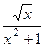более просто устроенную, но эквивалентную ей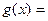 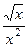, котрую можно записать в виде .

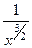Предел их отношения равен 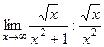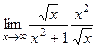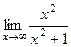1:

= = = 1.

Тогда сходимость первого интеграла равносильна сходимости второго, то есть можно рассматривать 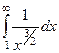. Степень 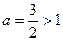, поэтому интеграл сходится.

Эти признаки позволяют сравнивать интегралы, содержащие громоздкие функции, с какими-то более простыми «эталонными», например, степенными.

Замечание. В прошлом примере мы рассматривали по старшей степени, а в аналогичной ситуации для интегралов 2 рода надо определять степень суммы по младшей степени. Для интегралов 2 рода верны аналогичные признаки сравнения, но в предельной форме сравнение происходит по наименьшей степени.

Кратные интегралы.

Определение. Пусть дана функция 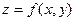, её область определения - некоторая область D в плоскости. Введём разбиение D на части двумя семействами прямых линий. В каждой части 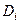возьмём произвольную точку 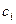с координатами 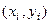. Площадь 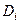обозначим 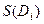. Величина 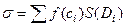называется интегральной суммой. Предел этой величины при измельчении разбиения называется двойным интегралом функции 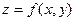по множеству 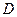, и обозначается .

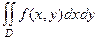Как правило, сначала будем рассматривать область D - прямоугольник: , .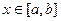

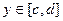Геометрический смысл. Интегральная сумма означает сумму объёмов параллелепипедов, построенных на каждом из оснований 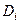, а интеграл - объём под поверхностью, которая задана уравнением .

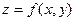Физический смысл. Если функция задаёт плотность какой-либо плоской пластины, то двойной интеграл - масса.

Аналогично определяется понятие тройного интеграла. Если дана функция 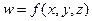, определённая в трёхмерной области, то её можно разбить на части с помощью трёх семейств плоскостей, выбрать по точке в каждой части, и составить интегральную сумму. То, что получается в пределе, называется тройным интегралом. 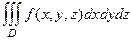. Физический смысл тройного интеграла: если функция - плотность некоторой породы, то в результате вычисления тройного интеграла получится масса.

Метод вычисления.

При вычислении кратных интегралов, как двойных, так и тройных, сводят к так называемым «повторным» интегралам.

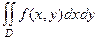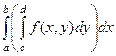= . Также в этом случае можно применять запись вида: 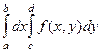где дифференциал пишется именно после того интеграла, которому он соответствует. При фиксировании одной переменной, мы получаем функцию уже не двух, а одной переменной. Так, при получается 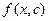. На чертеже этому соответствует сечение поверхности вдоль оси , то есть кривая. Интеграл по одной переменной при фиксированной второй, это площадь криволинейной трапеции, которая получается в сечении.

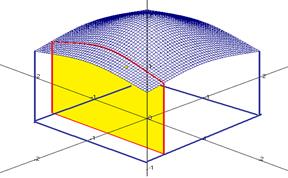
Если проинтегрировать все эти величины по второму направлению, то получится объём тела под поверхностью.

Аналогично, если разрезать булку хлеба на очень тонкие слои, а затем вычислить площадь каждого, и сложить все эти величины, умножая при этом на их толщину, то получим объём.

Пример. Вычислить интеграл 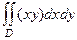, где 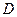есть квадрат: , .

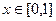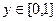Решение. 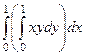= 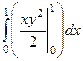вычислили сначала «частную первообразную» по переменной 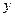, то есть ту функцию, частная производная от которой по 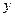была бы 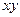. Во внутренних скобках применяем формулу Ньютона-Лейбница по переменной .

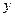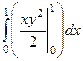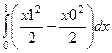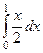= = . Оставшийся интеграл по переменной 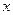вычисляется обычным образом: = = .

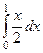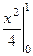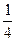Однако, область D может быть и не прямоугольной. Аналогично тому, как массив в программировании может быть не прямоугольным, тогда во внутреннем цикле двойного цикла границы переменные и зависят от переменной, определённой во внешнем цикле:

for i : = 1 to 10 do

for j : = 1 to i do

read (a[i,j]);

end;

end;

В случае, если область не прямоугольная, границы вложенного интеграла могут быть не числами, а зависеть от внешней переменной. Рассмотрим пример.

Пример.Вычислить 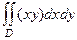, где 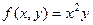, D - треугольник с вершинами (0,0), (1,0), (1,1).

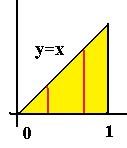
Решение.Границы фигуры по переменной 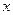это 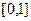, при других значениях 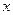нет точек этого треугольника вообще. При каждом 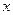, вертикальный отрезок имеет разную высоту, сначала вообще 0, а затем чем правее, тем больше. Чем больше 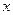, тем выше отрезок по 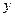. Вертикальные отрезки внутри треугольника от высоты 0 доходят до линии 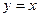. Поэтому при каждом 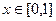, верно .

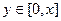Интеграл будет записан в виде: .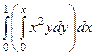

Граница во внутреннем интеграле зависит от внешней переменной .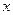

Границы внешнего интеграла обязательно должны быть контантами.

Во вложенной скобке, вычислится первообразная по , и будет применена формула Ньютона-Лейбница по .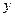

= = = .

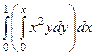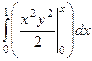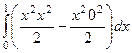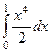И хотя границы зависят от 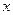, они подставлены в переменную 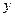, т.е. всё равно получилась функция от 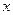, так же, как если был бы прямоуголник и границы были бы числовыми. Далее, уже обычным путём вычислим интеграл по 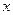.Итак, = = .

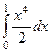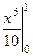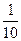ЛЕКЦИЯ № 5. 14.03.2017