Интегрирование по частям в неопределенном интеграле.

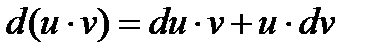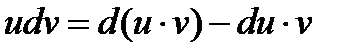Т.к. Þ . Проинтегрируем обе части равенства:

.

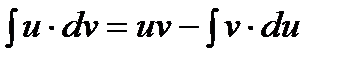Интегрирование по частям применяют, когда сложный интеграл можно заменить интегрированием более простого. Рассмотрим применение метода в следующих случаях:

1. Подынтегральная функция представляет собой произведение многочлена на показательную функцию или тригонометрическую. За u берется многочлен, за dv – оставшуюся часть подынтегрального выражения.

Пример1:

= =

= = .

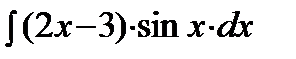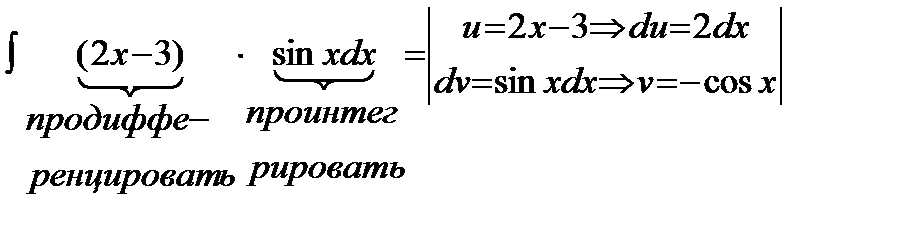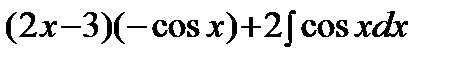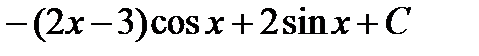Пример2:

= = =

= = .

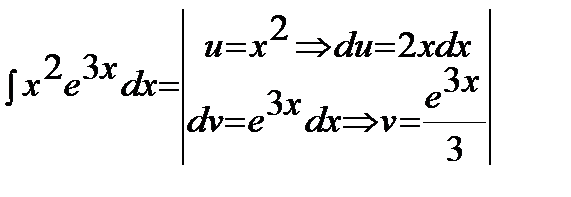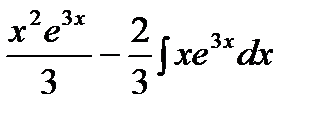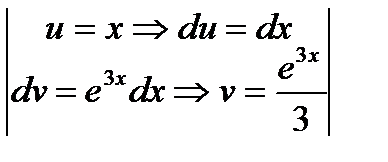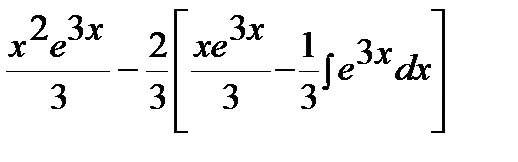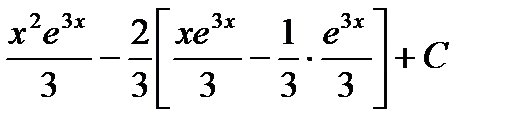2. Подынтегральная функция представляет собой произведение многочлена на логарифмическую или обратную тригонометрическую функцию. За часть u нужно взять логарифмическую или обратную тригонометрическую функцию.

Пример3:
= = = = = .

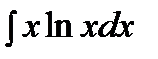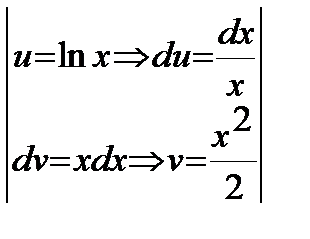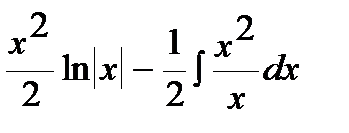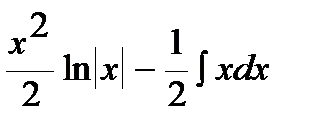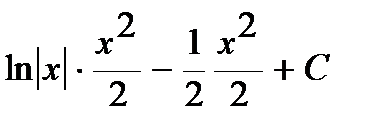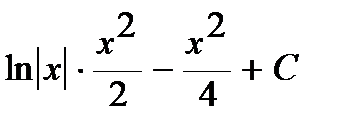Пример4:

= = = .

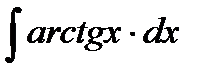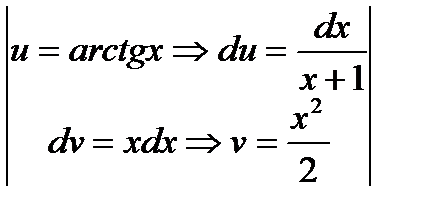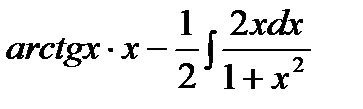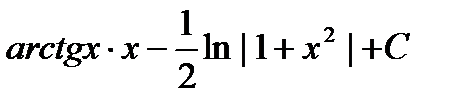3. Подынтегральная функция представляет собой произведение тригонометрической на показательную функцию. Не важно что брать за u.

Пример5:
I= = = = = .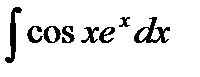

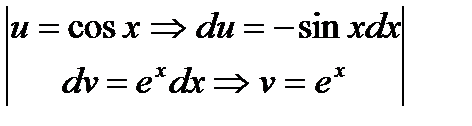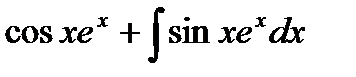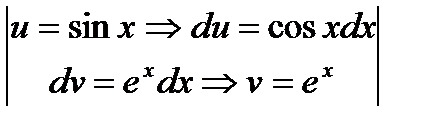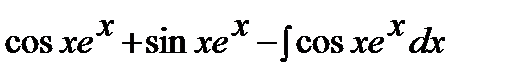Последний интеграл есть не что иное как исходный интеграл, поэтому можно

записать:

; ; .

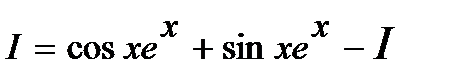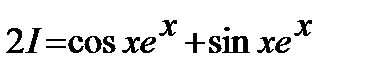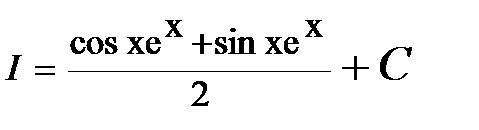4. Иногда метод интегрирования по частям приходится применять несколько раз.

Пример 6:

=

= = =

=

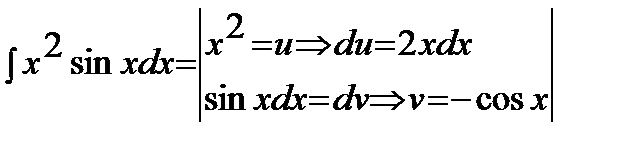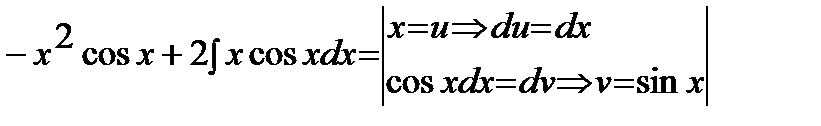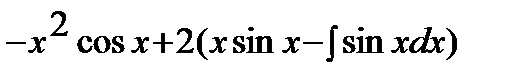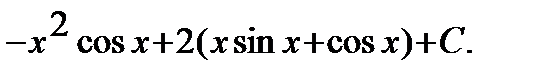
5. Если неверно выбраны u и dv, то в результате интегрирования получим более сложное выражение под интегралом, чем в исходном.

Пример 7:

= + …,

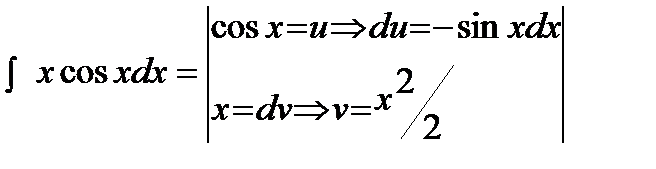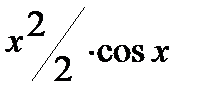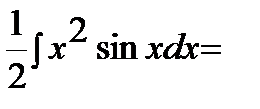отсюда видно, что полученный интеграл сложнее исходного.