Двойной интеграл. Задача об объеме цилиндрического тела.
К определенному интегралу мы пришли от задачи о площади криволинейной трапеции. К двойному интегралу мы приходим, решая задачу об объеме цилиндрического тела.
- Рассмотрим, например, прямой круговой цилиндр с высотой h и радиусом основания R его объем равен 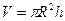
- Объем цилиндра той же высоты, в основании которого лежит эллипс с полуосями 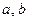 равен
равен 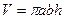 .
.
- Объем цилиндра той же высоты, с площадью основания 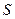 , равен
, равен 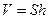 .
.
Пусть надо вычислить объем цилиндрического тела, в основании которого лежит область 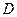 с площадью
с площадью 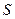 , а высота
, а высота 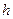 изменяется от точки к точке так, что конец ее описывает некоторую поверхность
изменяется от точки к точке так, что конец ее описывает некоторую поверхность 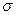 (
( 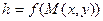 ). Тогда логично разбить область
). Тогда логично разбить область 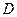 на области малого размера – организовать разбиение области на области – элементы разбиения. На каждом элементе отметим точку M(x,y) и построим над этим элементом прямой круговой цилиндр, высота которого постоянна для всех точек элемента и равна
на области малого размера – организовать разбиение области на области – элементы разбиения. На каждом элементе отметим точку M(x,y) и построим над этим элементом прямой круговой цилиндр, высота которого постоянна для всех точек элемента и равна 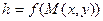 . Вычислим объем этого элементарного цилиндра. Просуммируем объемы всех элементарных цилиндров. Эта сумма и даст приближенно искомый объем цилиндрического тела тем точнее, чем меньше будут размеры элементов разбиения. Этот алгоритм используем для построения двойного интеграла
. Вычислим объем этого элементарного цилиндра. Просуммируем объемы всех элементарных цилиндров. Эта сумма и даст приближенно искомый объем цилиндрического тела тем точнее, чем меньше будут размеры элементов разбиения. Этот алгоритм используем для построения двойного интеграла
Двойной интеграл[1]
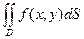 .
.
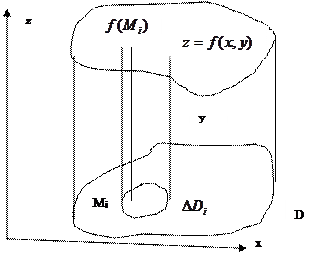  
| 1. Организуем разбиение области D на элементы – области 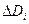 так, чтобы эти элементы не имели общих внутренних точек и так, чтобы эти элементы не имели общих внутренних точек и 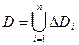 (условие А)
2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции (условие А)
2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции 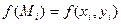 3. Построим интегральную сумму
3. Построим интегральную сумму 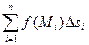 , где , где 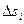 - площадь - площадь 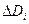 4. Переходя к пределу при условии
4. Переходя к пределу при условии 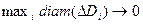 (условие В), получим двойной интеграл как предел интегральных сумм: (условие В), получим двойной интеграл как предел интегральных сумм: 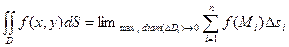
|
Теорема существования[2].
Пусть функция 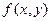 непрерывна в замкнутой односвязной области D[3]. Тогда двойной интеграл существует как предел интегральных сумм.
непрерывна в замкнутой односвязной области D[3]. Тогда двойной интеграл существует как предел интегральных сумм.
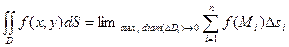 .
.
Замечание[4]. Предел этот не зависит от
- способа выбора разбиения, лишь бы выполнялось условие А
- выбора «отмеченных точек» на элементах разбиения,
- способа измельчения разбиения, лишь бы выполнялось условие В
Свойства двойного интеграла[5].
1. Линейность
а) свойство суперпозиции 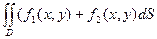 .=
.=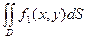 +
+ 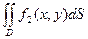
б) свойство однородности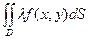 .=
.=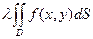
Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Они равны интегральным суммам для правых частей равенств, так как число слагаемых конечно. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.
2. Аддитивность.
Если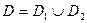 ,то
,то 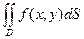 =
= 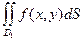 +
+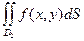
Доказательство. Выберем разбиение области D так, чтобы ни один из элементов разбиения (первоначально и при измельчении разбиения) не содержал одновременно как элементы D1, так и элементы D2. Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1.
3. 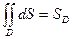 -площадь области D.
-площадь области D.
4. Если в области D выполнено неравенство 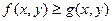 , то
, то 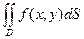
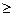
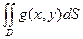 (неравенство можно интегрировать).
(неравенство можно интегрировать).
Доказательство. Запишем неравенство для интегральных сумм и перейдем к пределу.
Заметим, что, в частности, возможно 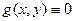
5. Теорема об оценке.
Если существуют константы 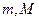 , что
, что 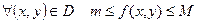 , то
, то
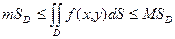
Доказательство. Интегрируя неравенство 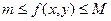 (свойство 4), получим
(свойство 4), получим 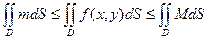 . По свойству 1 константы
. По свойству 1 константы 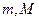 можно вынести из-под интегралов. Используя свойство 3, получим искомый результат.
можно вынести из-под интегралов. Используя свойство 3, получим искомый результат.
6. Теорема о среднем(значении интеграла).
Существует точка 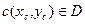 , что
, что 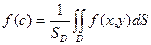 .
.
Доказательство. Так как функция 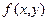 непрерывна на замкнутом ограниченном множестве
непрерывна на замкнутом ограниченном множестве 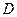 , то существует ее нижняя грань
, то существует ее нижняя грань 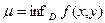 и верхняя грань
и верхняя грань 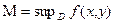 . Выполнено неравенство
. Выполнено неравенство 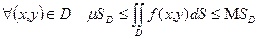 . Деля обе части на
. Деля обе части на 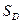 , получим
, получим 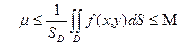 . Но число
. Но число 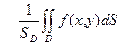 заключено между нижней и верхней гранью функции. Так как функция
заключено между нижней и верхней гранью функции. Так как функция 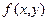 непрерывна на замкнутом ограниченном множестве
непрерывна на замкнутом ограниченном множестве 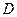 , то в некоторой точке
, то в некоторой точке 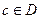 функция должна принимать это значение. Следовательно,
функция должна принимать это значение. Следовательно, 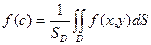 .
.
Геометрический смысл теоремы состоит в том, что существует цилиндр постоянной высоты 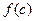 , объем которого равен объему цилиндрического тела
, объем которого равен объему цилиндрического тела 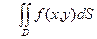
Дата добавления: 2017-11-21; просмотров: 2131;











