Неопределенный интеграл
Функция F(х) является первообразной для функции f(х) на заданном промежутке, если для всех значений х из заданого промежутка выполняется условие:
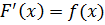
Если функция F(х) – первообразная для функции f(x), то множество функций F(x) + C , где С – произвольная постоянная, называется неопределенным интегралом от функции f(х) и обозначается
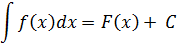
где f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, х – переменная интегрирования.
Свойства неопределенного интеграла:
1. 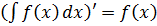
2. 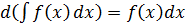
3. 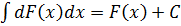
4. 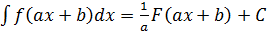
5. 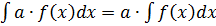
Формулы интегрирования:
1. 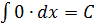
2. 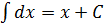
3. 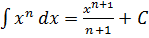
4. 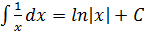
5. 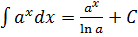
6. 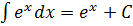
7. 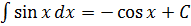
8. 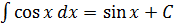
9. 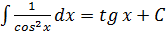
10. 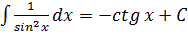
11. 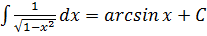
12. 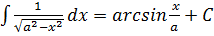
13. 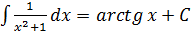
14. 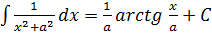
Методы интегрирования:
1. Непосредственное интегрирование. То есть интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
2. Если подынтегральная функция является дробью, у которой числитель есть производная от знаменателя, то интеграл равен натуральному логарифму от знаменателя.
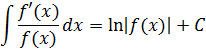
3. Метод замены переменной. То есть переменная интегрирования заменяется новой переменной в результате чего интеграл переходит в другой интеграл, более простой, чем начальный.
Пример.Вычислить неопределенный интеграл
А) Метод непосредственного интегрирования (используя формулы интегрирования):
1) 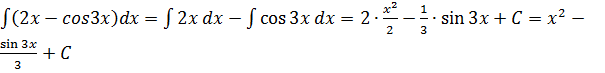 .
.
2) 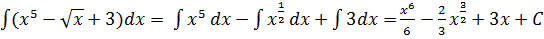 .
.
3) 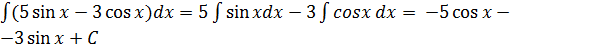 .
.
4) 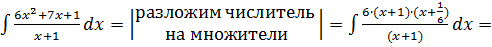
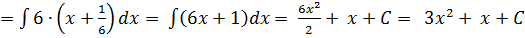 .
.
Б) Если числитель подынтегральной функции f(x) равен производной знаменателя:
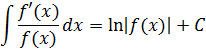
5 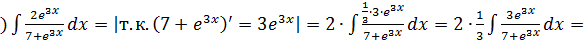
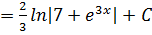 .
.
В) Метод замены переменной (метод подстановки):
6) 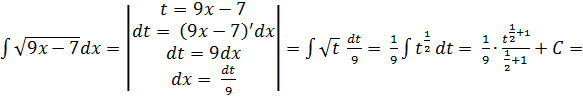
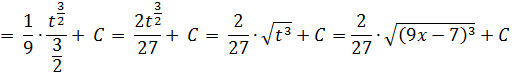
7) 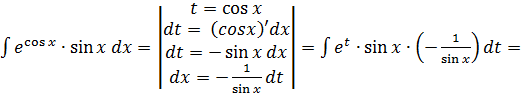
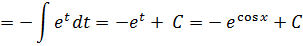
Дата добавления: 2016-06-05; просмотров: 2502;











