Первообразная и неопределённый интеграл

Основной задачей дифференциального исчисления является нахождение производной f '(x) или дифференциала f '(x)dx данной функции f(x)
В интегральном исчислении решается обратная задача:
Дана функция f(x); требуется найти такую функцию F(x), производная которой равна f(x) или дифференциал которой равен f(x)dx в области определения функции f(x), т.е. в этой области функции f(x) и F(x) связаны соотношением

F'(x)=f(x)

или

dF(x)= F'(x)dx= f(x)dx

Определение 1: Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x) выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx
Из дифференциального исчисления известно что если две функции f(x) и j(x) отличаются друг от друга на постоянную величину, то производные или дифференциалы этих функций равны, т.е. если

f(x) = j(x) + C

то

f '(x) = j'(x)

или

f '(x)dx = j'(x)dx

Известно также, что, и наоборот, если две функции f(x) и j(x) имеют одну и ту же производную или один и тот-же дифференциал, то они отличаются друг от друга на постоянную величину, т.е. если

f '(x) = j'(x) или df(x) = dj(x),

то

f(x) = j(x) + С

Отсюда непосредственно следует, что если в формуле y = F(x) + C мы будем придавать постоянной C все возможные значения, то получим все возможные первообразные функции для функции f (x)
Определение 2: Множество F(x) + C всех первообразных функций для данной функции f (x) , где C принимает все возможные числовые значения, называется неопределенным интегралом от функции f (x) и обозначается символом

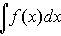
Таким образом, по определению,

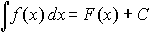
где F'(x) = f (x) или dF(x) = f(x)dx иС- произвольная постоянная. В последней формуле f(x) называется подинтегральной функцией, f(x)dx- подинтегральным выражением, а символ 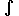- знаком неопределенного интеграла.
Неопределенным интегралом называют не только множество всех первообразных, но и любую функцию этого множества.
Таким образом, неопределенный интеграл представляет собой любую функцию, дифференциал которой равен подинтегральному выражению, а производная равна подинтегральной функции
Нахождение первообразной по данной функции f(x) называется интегрированием и является действием, обратным дифференцированию.

Свойства неопределённого интеграла. Таблица элементарных интегралов

iСвойства неопределенного интеграла базируются на свойствах дифференциала функции.

Напомним, что если 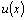– дифференцируемая в точке 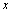функция, то произведение

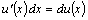является дифференциалом функции 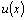в точке 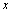соответственно приращению аргумента .

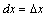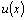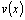Для дифференцируемых функций и правила действий над их дифференциалами аналогичны правилам вычисления производных (здесь и везде далее 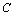– произвольное число), а именно:

;

; ;

; ;

.

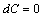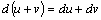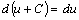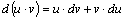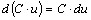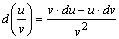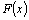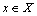Для первообразной функции из соотношения , имеем 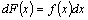или 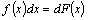– подведение функции под дифференциал.

Используя указанные равенства, получаем следующие свойства неопределенного интеграла.

Свойство 1. ,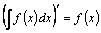

т.е. производная неопределенного интеграла (производная каждой функции множества всех первообразных 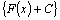) равна подынтегральной функции.

Свойство 2. ,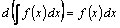

т.е. дифференциал неопределенного интеграла (дифференциал
каждой функции множества всех первообразных) равен подынтегральному выражению.

Иначе, знаки дифференциала и интеграла взаимно уничтожаются, если знак " 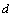" стоит перед знаком " ".

Свойство 3. ,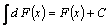

т.е. неопределенный интеграл от дифференциала какой-либо функции равен сумме этой функции и произвольного числа 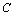. Иначе, если знак " " стоит рядом и перед знаком " 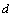", то эти знаки тоже взаимно уничтожаются, причем к функции 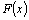прибавляется произвольное число .

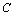Свойство 4. –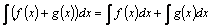

аддитивность по функции операции интегрирования, т.е. неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от этих функций (предполагается, что все участвующие в равенстве интегралы существуют). При этом, есл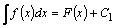и и 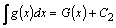, то записывают 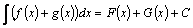, объединяя 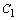и 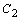в одну произвольную постоянную .

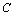Свойство 4 верно для суммы конечного множества слагаемых.

Свойство 5. , , –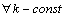

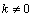Однородность операции интегрирования, т.е. при вычислении неопределенного интеграла постоянный ненулевой множитель можно
выносить за знак интеграла (соответственно можно вносить под знак интеграла).

Таблица элементарных интегралов

ВОПРОС 42. Интегрирование заменой переменной. Интегрирование методом подстановки.

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т. е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл 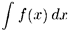. Сделаем подстановку 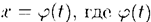– функция, имеющая непрерывную производную.
Тогда 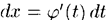и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой

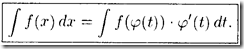(23.1)

Формула (23.1) также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла правой части этого равенства следует перейти от повой переменной интегрирования t назад к переменной х.
Иногда целесообразно подбирать подстановку в виде 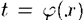,тогда .Другими словами, формулу (23.1) можно применять справа налево.

ВОПРОС 43. Интегрирование по частям.

ВОПРОС 44. Рациональные функции. Разложение рациональных функций на сумму элементарных дробей. Интегрирование элементарных дробей.

ВОПРОС 45. Задача о вычислении площади плоской фигуры. Определённый интеграл Римана. Свойства определённого интеграла.

ВОПРОС 46. Формула Ньютона-Лейбница. Интегралы по симметричным промежуткам от чётных и нечётных функций. Оценки интегралов. Интегрально среднее.

Простым и удобным методом вычисления определенного интеграла 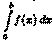от непрерывной функции является формула Ньютона-Лейбница:

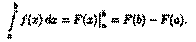
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции ƒ (х).

Например,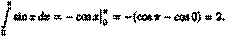

При вычисленииопределенных интегралов широко используется метод замены переменной и метод интегрирования по частям.

39.2. Интегрирование подстановкой (заменой переменной)

Пусть для вычисления интеграла 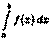от непрерывной функции

сделана подстановка х = φ(t).

Теорема 39.1. Если:

1) функция х = φ(t) и ее производная х' = φ'(t) непрерывны при t є [а;β];

2) множеством значений функции х = φ(t) при t є [а,β] является отрезок [а; b];

3) φ(а)=а и φ(β)=b.

то

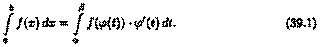
▼Пусть F(x) есть первообразная для ƒ(х) на отрезке [а;b]. Тогда по формуле Ньютона-Лейбница 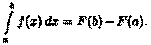Так как (F(φ(t))' = f(φ(t)) - φ'(t), то F(φ(t)) является первообразной для функции f(φ(t)) -φ'(t), t  [а;β]. Поэтому по формуле Ньютона—Лейбница имеем

▲

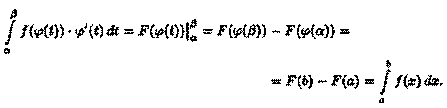Формула (39.1) называется формулой замены переменной в определенном интеграле. Отметим, что:

1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;

2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x);

3) не следует забывать менять пределы интегрирования при замене переменных!

Пример 39.1. Вычислить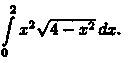

Решение: Положим х = 2 sin t, тогда dx = 2 cos t dt. Если х=0, то t = 0; если x = 2, то t = 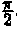. Поэтому

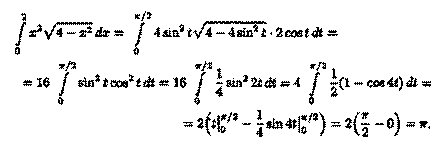
39.3. Интегрирование по частям

Теорема 39.2. Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула

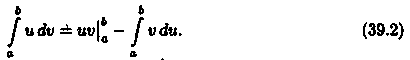
▼На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:

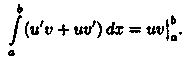
Следовательно,

▲

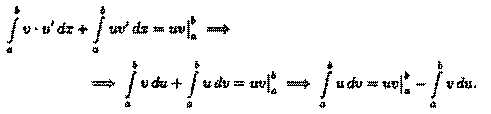Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.

Пример 39.2. Вычислить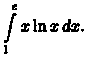

Решение: Положим

Применяя формулу (39.2), получаем

Пример 39.3. Вычислить интеграл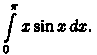

Решение: Интегрируем по частям. Положим

Поэтому

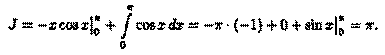
39.4. Интегрирование четных и нечетных функций в симметричных пределах

Пусть функция ƒ(х) непрерывна на отрезке [-а; а], симметричном относительно точки х = 0. Докажем, что

▼Разобьем отрезок интегрирования [-а; а] на части [-а; 0] и [0; а]. Тогда по свойству аддитивности

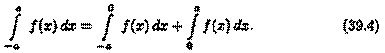
В первом интеграле сделаем подстановку х = -t. Тогда

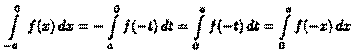
(согласно свойству: «определенный интеграл не зависит от обозначения переменной интегрирования»). Возвращаясь к равенству (39.4), получим

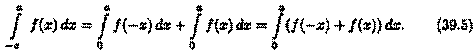
Если функция ƒ(х) четная (ƒ(-х) = ƒ(х)), то ƒ(-х) + ƒ(х) = 2ƒ(х); если функция ƒ(х) нечетная (ƒ(-х) = - ƒ(х)), то ƒ(-х) + ƒ(х) = 0. Следовательно, равенство (39.5) принимает вид (39.3).▲

Благодаря доказанной формуле можно, например, сразу, не производя вычислений, сказать, что

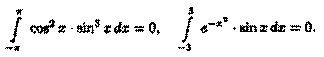
ВОПРОС 47. Интеграл с переменным верхним пределом. Интегралы по бесконечным промежуткам.