Интегрирование некоторых иррациональных алгебраических функций.
Пусть 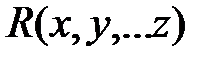 - рациональная функция своихаргументов. Тогда интеграл
- рациональная функция своихаргументов. Тогда интеграл 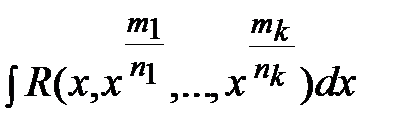 находится заменой переменных
находится заменой переменных 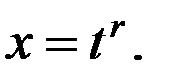
Как правило, за 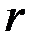 берется наименьшее общее кратное чисел
берется наименьшее общее кратное чисел 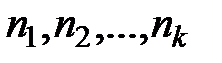 , где
, где 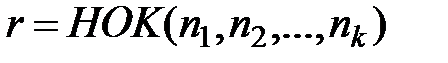 , т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.
, т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.
Пример 1. Вычислить неопределенный интеграл 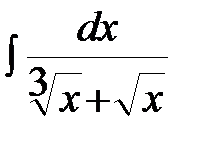 .
.
Решение:
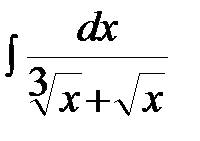
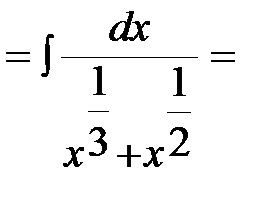
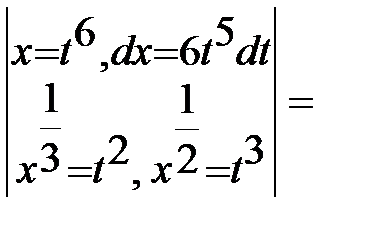
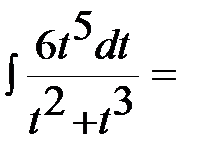
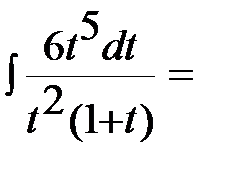
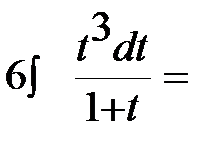
В подынтегральном выражении выделим целую часть: 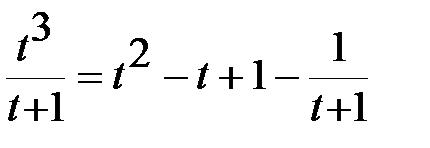 ,
,
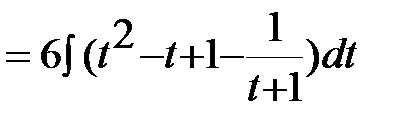
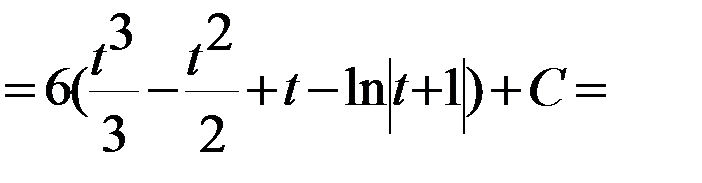
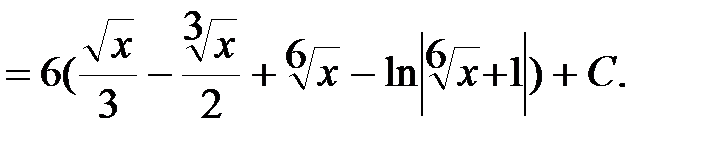
В некоторых случаях проинтегрировать иррациональные выражения помогают тригонометрические подстановки:
1) 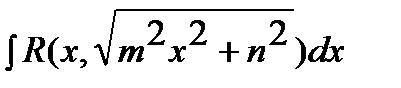 .
.
Такие выражения рационализируются с помощью следующей подстановки
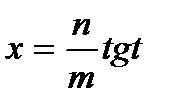 ,
, 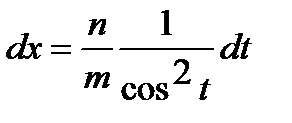 .
.
Пример 2. Найти неопределенный интеграл 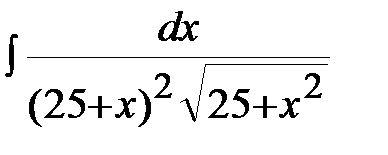 .
.
Замена 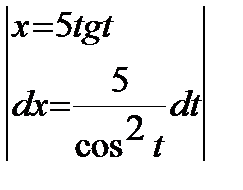 .
.
Интеграл примет вид: 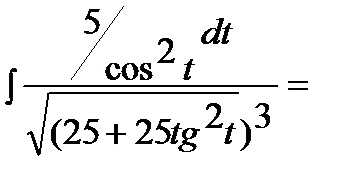
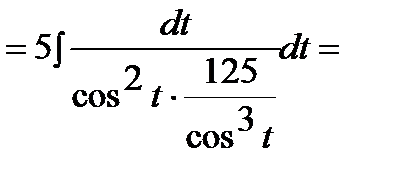
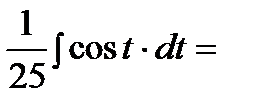
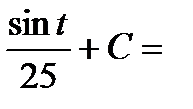
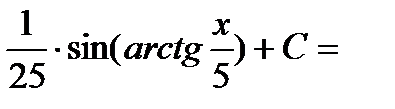
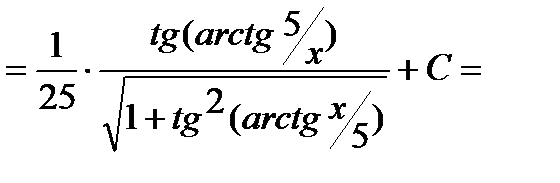
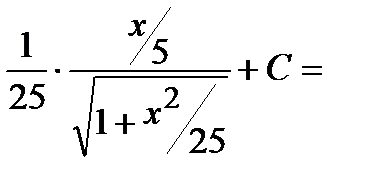
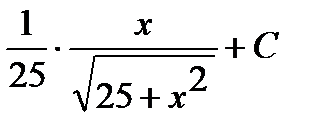 .
.
2) 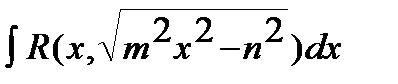
Такие выражения рационализируются с помощью следующей подстановки
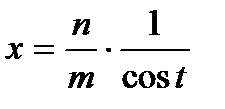 ,
, 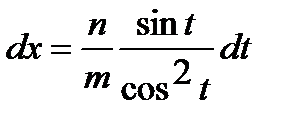 .
.
Пример 3. Найти неопределенный интеграл 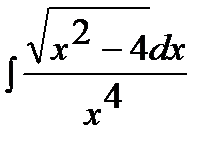 .
.
Замена 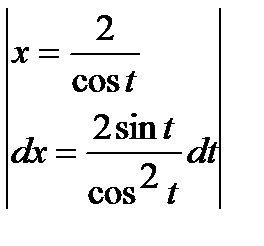 .
.
Тогда 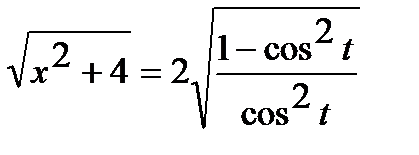
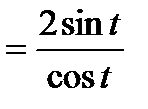 .
.
Интеграл примет вид: 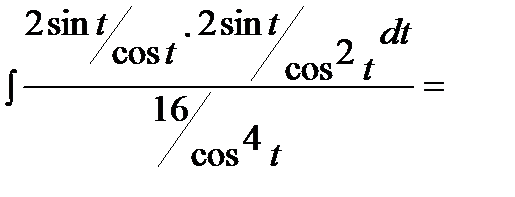
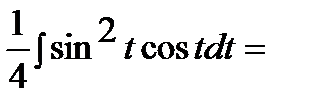
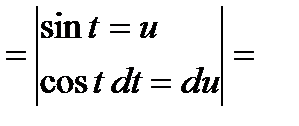
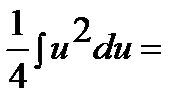
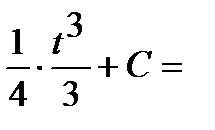
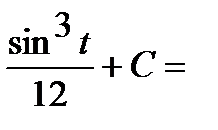
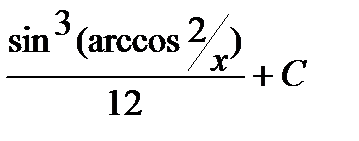
3) 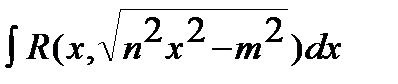 .
.
Такие выражения рационализируются с помощью следующей подстановки
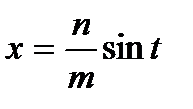 ,
, 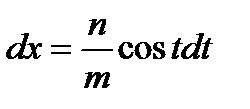 .
.
Пример 4. Найти неопределенный интеграл 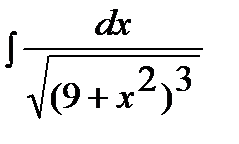 .
.
Замена 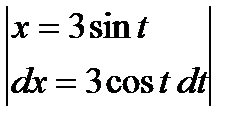 .
.
Тогда интеграл примет вид: 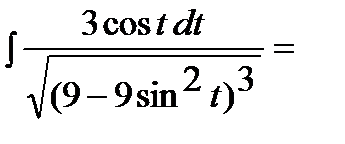
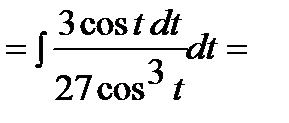
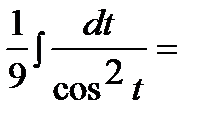
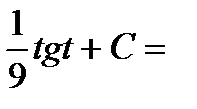
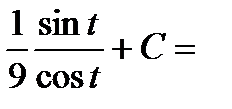
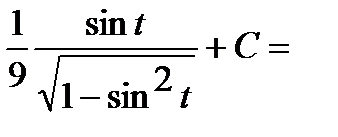
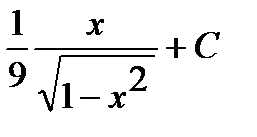 .
.
Интегрирование тригонометрических выражений.
Пусть 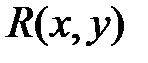 — рациональная функция своих аргументов. Рассмотрим несколько случаев:
— рациональная функция своих аргументов. Рассмотрим несколько случаев:
Й случай.
Интеграл 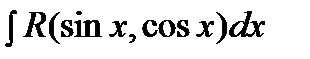 универсальной тригонометрической подстановкой
универсальной тригонометрической подстановкой 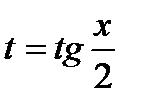 сводится к интегралу от рациональной функции. При этом
сводится к интегралу от рациональной функции. При этом 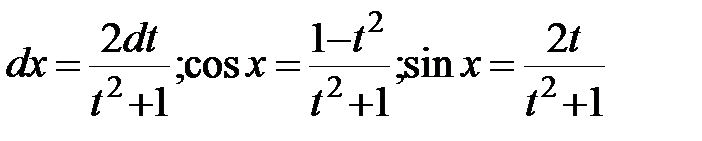 .
.
С учетом сделанной замены получим
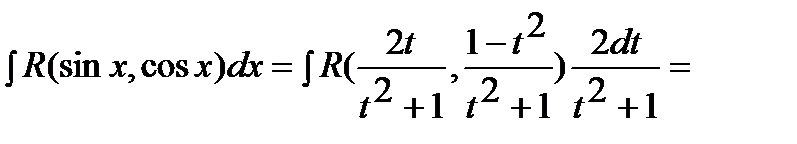
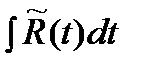 ,
,
где 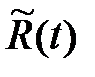 - рациональная функция, интеграл от которой рассматривался выше.
- рациональная функция, интеграл от которой рассматривался выше.
Пример: Найти неопределенный интеграл: 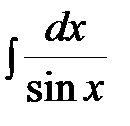 .
.
Решение: Сделаем универсальную тригонометрическую подстановку:
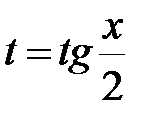 ;
; 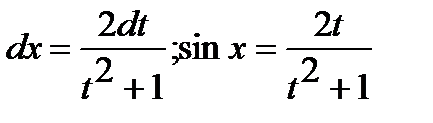 .
.
Тогда 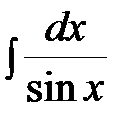
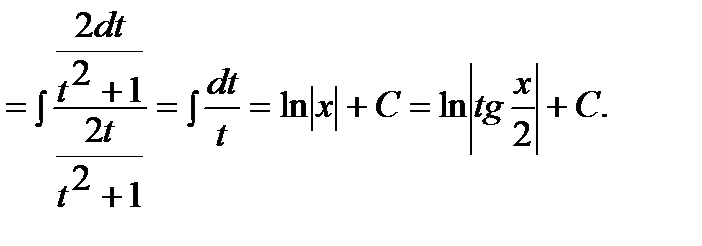 .
.
Отметим, что универсальную тригонометрическую подстановку, как правило, используют в тех случаях, когда другие подстановки, приведенные ниже не приводят к желаемым результатам.
Й случай.
В интегралах 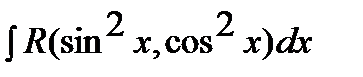 , где
, где 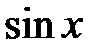 и
и 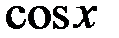 входят в подынтегральную рациональную функцию, только в четных степенях делается замена
входят в подынтегральную рациональную функцию, только в четных степенях делается замена 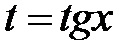 . При этом
. При этом
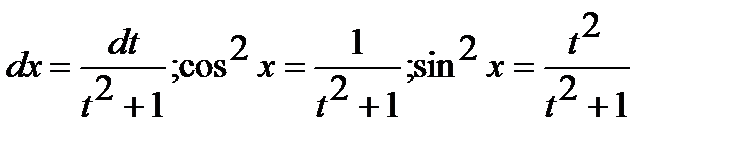 .
.
Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида 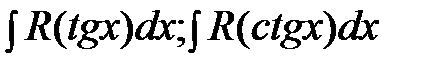 .
.
Пример: Найти неопределенный интеграл:
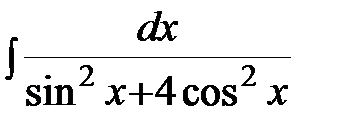 .
.
Решение: Сделаем подстановку:
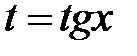 ;
; 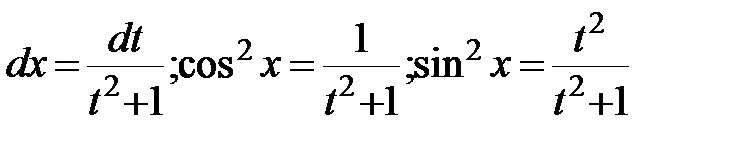 .
.
Тогда 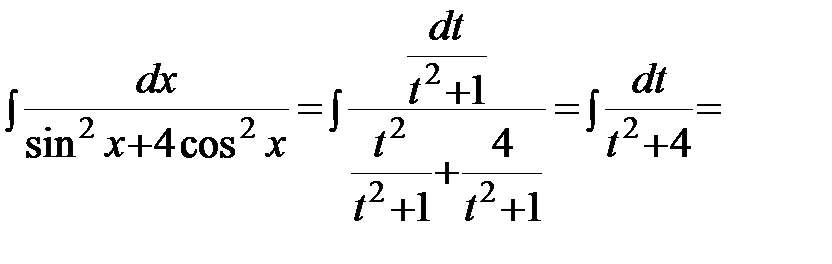
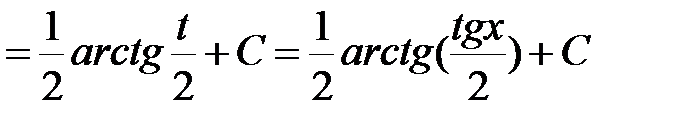 .
.
Пример. Найти неопределенный интеграл: 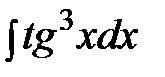 .
.
Решение: 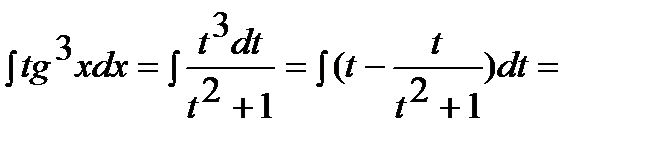

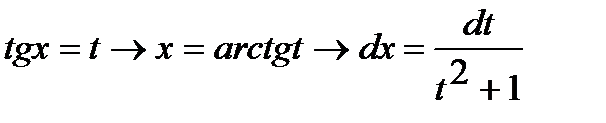
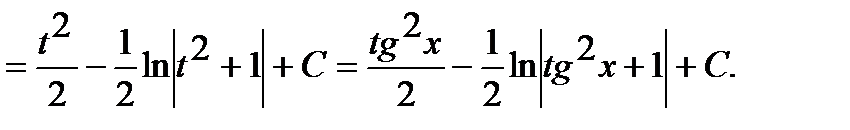
3-й случай. Интегрирование выражений вида
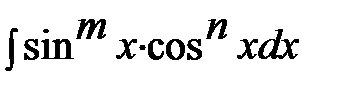 , (6)
, (6)
где mи n-целые числа. Рассмотрим два случая:
а) Среди чисел m,nесть хотя бы одно нечетное. Тогда за tпринимается функция, стоящая в основании другой степени.
Пример. Найти неопределенный интеграл:
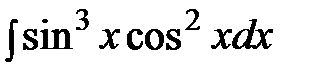 .
.
Решение: Здесь функция 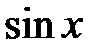 стоит в нечетной степени, поэтому
стоит в нечетной степени, поэтому 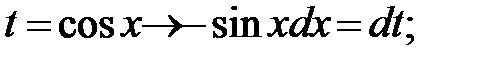
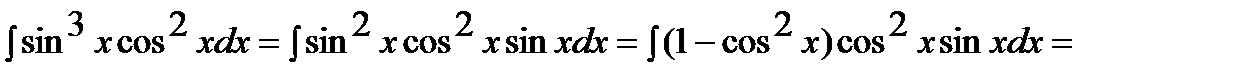
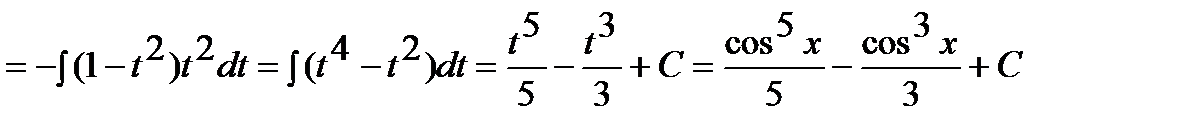 ;
;
б) В выражении (6) оба числаm,n- четные неотрицательные.
Положим m=2p, n=2q и применим формулы:
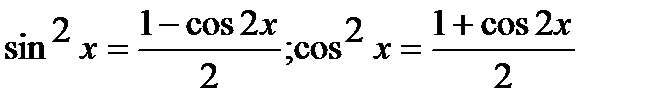 .
.
Тогда 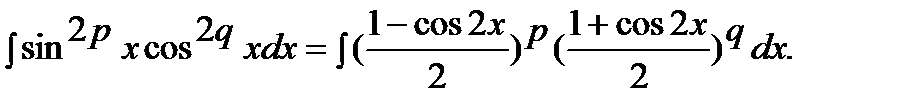
Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:
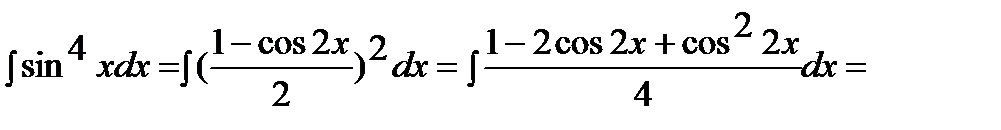
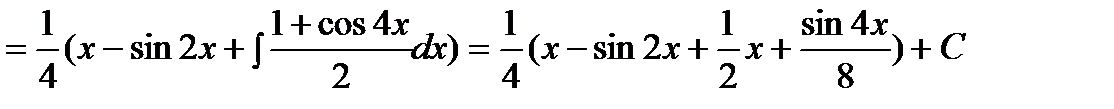 .
.
Дата добавления: 2016-06-05; просмотров: 2035;











