Лекция 4. Понятие комплексного числа.
Комплексным числом называется выражение вида 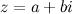
Например. 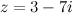
Действительная и мнимая часть комплексного числа
Действительное число  называется действительной частью комплексного числа
называется действительной частью комплексного числа 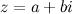 и обозначается
и обозначается 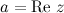 (От французского слова reel - действительный).
(От французского слова reel - действительный).
Действительное число 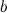 называется мнимой частью числа
называется мнимой частью числа 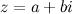 и обозначается
и обозначается 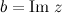 (От французского слова imaginaire - мнимый).
(От французского слова imaginaire - мнимый).
Например. Для комплексного числа 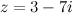 действительная часть
действительная часть 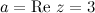 , а мнимая -
, а мнимая - 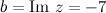 .
.
Если действительная часть комплексного числа 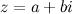 равна нулю (
равна нулю ( 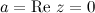 ), то комплексное число называется чисто мнимым.
), то комплексное число называется чисто мнимым.
Например. 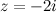
Мнимая единица
Величина 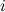 называется мнимой единицей и удовлетворяет соотношению:
называется мнимой единицей и удовлетворяет соотношению:

Равные комплексные числа
Два комплексных числа 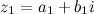 и
и 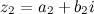 называются равными, если равны их действительные и мнимые части соответственно:
называются равными, если равны их действительные и мнимые части соответственно:
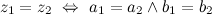
Задание. Определить при каких значениях  и
и 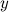 числа
числа 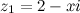 и
и 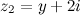 будут равными.
будут равными.
Решение. Согласно определению 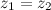 тогда и только тогда, когда
тогда и только тогда, когда
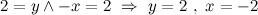
Ответ. 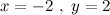
Число 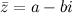 называется комплексно сопряженным числом к числу
называется комплексно сопряженным числом к числу 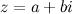 .
.
То есть комплексно сопряженные числа отличаются лишь знаком мнимой части.
Например. Для комплексного числа 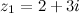 комплексно сопряженным есть число
комплексно сопряженным есть число 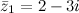 ; для
; для 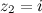 комплексно сопряженное
комплексно сопряженное 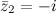 и для
и для 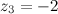 имеем, что
имеем, что 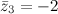 .
.
Комплексное число 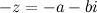 называется противоположным к комплексному числу
называется противоположным к комплексному числу 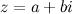 .
.
Например. Противоположным к числу 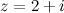 есть число:
есть число: 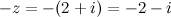 .
.
Сложение комплексных чисел
Суммой двух комплексных чисел 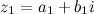 и
и 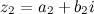 называется комплексное число
называется комплексное число  , которое равно
, которое равно
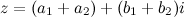
То есть суммой двух комплексных чисел есть комплексное число, действительная и мнимая части которого есть суммой действительных и мнимых частей чисел-слагаемых соответственно.
Задание. Найти сумму 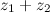 , если
, если 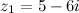 ,
, 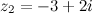 .
.
Решение. Искомая сумма равна
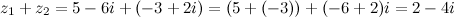
Ответ. 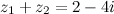
Вычитание комплексных чисел
Разностью двух комплексных чисел 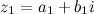 и
и 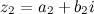 называется комплексное число
называется комплексное число 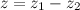 , действительная и мнимая части которого есть разностью действительных и мнимых частей чисел
, действительная и мнимая части которого есть разностью действительных и мнимых частей чисел 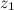 и
и 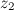 соответственно:
соответственно:
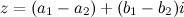
Задание. Найти разность 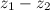 , если
, если 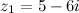 ,
, 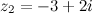 .
.
Решение. Действительная часть искомого комплексного числа равна разности действительных частей чисел 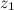 и
и 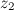 , а мнимая - мнимых частей этих чисел, то есть
, а мнимая - мнимых частей этих чисел, то есть
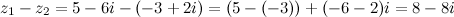
Ответ. 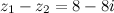
Произведением двух комплексных чисел 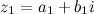 и
и 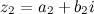 называется комплексное число
называется комплексное число  , равное
, равное
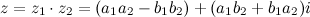
На практике чаще всего комплексные числа перемножают как алгебраические двучлены 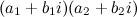 , просто раскрыв скобки, в полученном результате надо учесть, что
, просто раскрыв скобки, в полученном результате надо учесть, что 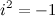 .
.
Задание. Найти произведение комплексных чисел 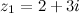 и
и 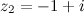 .
.
Решение. Перемножим заданные комплексные числа как два двучлена, то есть
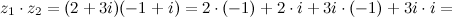
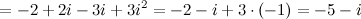
Ответ. 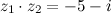
Комплексно сопряженные числа
Если 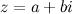 , то число
, то число 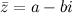 называется комплексным сопряженным к числу
называется комплексным сопряженным к числу  .
.
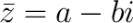
То есть у комплексно сопряженных чисел действительные части равны, а мнимые отличаются знаком.
Например. Комплексно сопряженным к числу 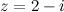 есть число
есть число 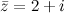 .
.
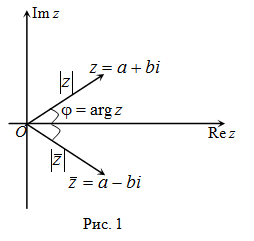
На комплексной плоскости комплексно сопряжённые числа получаются зеркальным отражением друг друга относительно действительной оси.
Свойства комплексно сопряженных чисел
1) Если 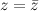 , то можно сделать вывод, что рассматриваемое число
, то можно сделать вывод, что рассматриваемое число  является действительным.
является действительным.
Например. 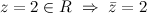 и
и 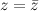
2) Для любого комплексного числа  сумма
сумма 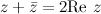 - действительное число.
- действительное число.
Например. Пусть 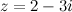 , тогда
, тогда 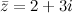 , а тогда
, а тогда
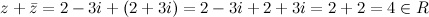
3) Для произвольного комплексного числа 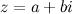 произведение
произведение 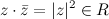 .
.
Например. Пусть 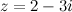 , комплексно сопряженное к нему число
, комплексно сопряженное к нему число 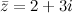 , тогда произведение
, тогда произведение
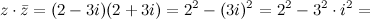
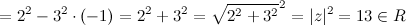
4) Модули комплексно сопряженных чисел равны: 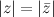 , а аргументы отличаются знаком (рис. 1).
, а аргументы отличаются знаком (рис. 1).
5) 
6) 
7) 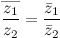
8) 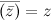
9) Если 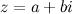 и
и 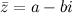 - комплексно сопряженные числа, то
- комплексно сопряженные числа, то
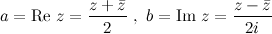
Дата добавления: 2016-06-05; просмотров: 3260;











