Лекция 3. Приближенное значение величины.

Для современных задач необходимо использовать сложный математический аппарат и развитые методы их решения. При этом часто приходится встречаться с задачами, для которых аналитическое решение, т.е. решение в виде аналитического выражения, связывающего исходные данные с требуемыми результатами, либо вообще невозможно, либо выражается такими громоздкими формулами, что использование их для практических целей нецелесообразно.

В этом случае применяются численные методы решения, которые позволяют достаточно просто получить численное решение поставленной задачи. Численные методы реализуются с помощью вычислительных алгоритмов.

Все многообразие численных методов подразделяют на две группы:

Точные – предполагают, что если вычисления ведутся точно, то с помощью конечного числа арифметических и логических операций могут быть получены точные значения искомых величин.

Приближенные– которые даже в предположении, что вычисления ведутся без округлений, позволяют получить решение задачи лишь с заданной точностью.

1. величина и число. Величиной называется то, что в определенных единицах может быть выражено числом.

Когда говорят о значении величины, то имеют в виду некоторое число, называемое числовым значением величины, и единицу ее измерения.

Таким образом, величиной называют характеристику свойства объекта или явления, которая является общей для множества объектов, но имеет индивидуальные значения для каждого из них.

Величины могут быть постоянными и переменными. Если при некоторых условиях величина принимает только одно значение и не может его изменять, то она называется постоянной, если же она может принимать различные значения, то – переменной. Так, ускорение свободного падения тела в данном месте земной поверхности есть величина постоянная, принимающая единственное числовое значение g=9,81… м/с2, в то время как путь s, проходимый материальной точкой при ее движении, – величина переменная.

2. приближенные значения чисел. Значение величины, в истинности которого мы не сомневаемся, называется точным. Часто, однако, отыскивая значение какой-либо величины, получают лишь ее приближенное значение. В практике вычислений чаще всего приходится иметь дело с приближенными значениями чисел. Так, p – число точное, но вследствие его иррациональности можно пользоваться лишь его приближенным значением.

Во многих задачах из-за сложности, а часто и невозможности получения точных решений применяются приближенные методы решения, к ним относятся: приближенное решение уравнений, интерполирование функций, приближенное вычисление интегралов и др.

Главным требованием к приближенным расчетам является соблюдение заданной точности промежуточных вычислений и конечного результата. При этом в одинаковой степени недопустимы как увеличение погрешностей (ошибок) путем неоправданного загрубления расчетов, так и удержание избыточных цифр, не соответствующих фактической точности.

Существуют два класса ошибок, получающихся при вычислениях и округлении чисел – абсолютные и относительные.

1. Абсолютная погрешность (ошибка).

Введем обозначения:

Пусть А – точное значение некоторой величины, Запись а » Абудем читать "а приближенно равно А". Иногда будем писать А = а, имея в виду, что речь идет о приближенном равенстве.

Если известно, что а < А, то а называют приближенным значением величины А с недостатком. Если а > А, то а называют приближенным значением величины А с избытком.

Разность точного и приближенного значений величины называется погрешностью приближения и обозначается D, т.е.

D = А – а (1)

Погрешность D приближения может быть как числом положительным, так и отрицательным.

Для того чтобы охарактеризовать отличие приближенного значения величины от точного, часто бывает достаточно указать абсолютную величину разности точного и приближенного значений.

Абсолютная величина разности между приближенным а и точным А значениями числа называется абсолютной погрешностью (ошибкой) приближения и обозначается D_а:

D_а = ½а – А½ (2)

Пример 1. При измерении отрезка l использовали линейку, цена деления шкалы которой равна 0,5 см. Получили приближенное значение длины отрезка а = 204 см.

Понятно, что при измерении могли ошибиться не более, чем на 0,5 см, т.е. абсолютная погрешность измерения не превышает 0,5 см.

Обычно абсолютная ошибка неизвестна, поскольку неизвестно точное значение числа А. Поэтому в качестве ошибки принимают какую-либо оценку абсолютной ошибки:

D_а <= D_{а пред.} (3)

где D_{а пред.} – предельная ошибка (число, большее нуля), задаваемая с учетом того, с какой достоверностью известно число а.

Предельная абсолютная погрешность называется также границей погрешности. Так, в приведенном примере,
D_{а пред.}= 0,5 см.

Из (3) получаем: D_а = ½а – А½<= D_{а пред.}. и тогда

а – D_{а пред.} ≤ А ≤ а + D_{а пред.}. (4)

Значит, а – D_{а пред.} будет приближенным значением А с недостатком, а а + D_{а пред} –приближенным значением А с избытком. Пользуются также краткой записью: А = а ± D_{а пред} (5)

Из определения предельной абсолютной погрешности следует, что чисел D_{а пред}, удовлетворяющих неравенству (3), будет бесконечное множество. На практике стараются выбратьвозможно меньшее из чисел D_{а пред}, удовлетворяющих неравенству D_а <= D_{а пред.}

Пример 2. Определим предельную абсолютную погрешность числа а=3,14, взятого в качестве приближенного значения числа π.

Известно, что 3,14<π<3,15.Отсюда следует, что

|а – π |< 0,01.

За предельную абсолютную погрешность можно принять число D_а = 0,01.

Если же учесть, что 3,14<π<3,142, то получим лучшую оценку: D_а = 0,002, тогда π ≈3,14 ±0,002.

Относительная погрешность (ошибка).Знания только абсолютной погрешности недостаточно для характеристики качества измерения.

Пусть, например, при взвешивании двух тел получены следующие результаты:

Р₁= 240,3 ±0,1 г.

Р₂= 3,8 ±0,1 г.

Хотя абсолютные погрешности измерения обоих результатов одинаковы, качество измерения в первом случае будет лучшим, чем во втором. Оно характеризуется относительной погрешностью.

Относительной погрешностью (ошибкой)приближения числа А называется отношение абсолютной ошибки D_а приближения к абсолютной величине числа А:

Так, как точное значение величины обычно неизвестно, то его заменяют приближенным значением и тогда:

Предельной относительной погрешностью или границей относительной погрешности приближения, называется число d_{а пред.}>0, такое, что:

d_а <= d_{а пред.}

За предельную относительную погрешность можно, очевидно, принять отношение предельной абсолютной погрешности к абсолютной величине приближенного значения:

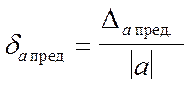
Из (9) легко получается следующее важное соотношение:

∆_{а пред .}= |a| d_{а пред.}

Предельную относительную погрешность принято выражать в процентах:

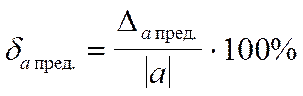
Пример. Основание натуральных логарифмов для расчета принято равным е=2,72. В качестве точного значения взяли е_т = 2,7183. Найти абсолютную и относительную ошибки приближенного числа.

D_е = ½е – е_т½=0,0017;

.

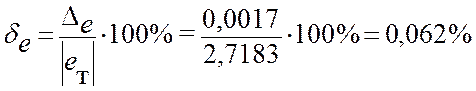Величина относительной ошибки остается неизменной при пропорциональном изменении самого приближенного числа и его абсолютной ошибки. Так, у числа 634,7, рассчитанного с абсолютной ошибкой D = 1,3 и у числа 6347 с ошибкой D = 13 относительные ошибки одинаковы: d = 0,2.