Лекция 7. Корни натуральной степени из числа.

Корнем степени n из действительного числа a, где n - натуральное число, называется такое действительное число x, n-ая степень которого равна a.

Корень степени n из числа a обозначается символом 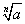. Согласно этому определению .

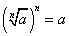Нахождение корня n-ой степени из числа a называется извлечением корня. Число аназывается подкоренным числом (выражением), n - показателем корня. При нечетном n существует корень n-ой степени для любого действительного числа a. При четном n существует корень n-ой степени только для неотрицательного числаa. Чтобы устранить двузначность корня n-ой степени из числа a, вводится понятие арифметического корня n-ой степени из числа a.

Понятие арифметического корня степени N

Если 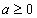и n - натуральное число, большее 1, то существует, и только одно, неотрицательное число х, такое, что выполняется равенство 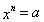. Это число хназывается арифметическим корнем n-й степени из неотрицательного числа а и обозначается 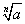. Число а называется подкоренным числом, n - показателем корня.

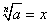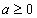Итак, согласно определению запись , где , означает, во-первых, что 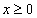и, во-вторых, что 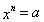, т.е. .

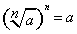Понятие степени с рациональным показателем

Степень с натуральным показателем: пусть а - действительное число, а n - натуральное число, большее единицы, n-й степенью числа а называют произведение n множителей, каждый из которых равен а, т.е. 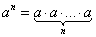. Число а - основание степени, n - показатель степени. Степень с нулевым показателем: полагают по определению, если 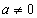, то 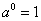. Нулевая степень числа 0 не имеет смысла. Степень с отрицательным целым показателем: полагают по определению, если 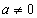и n - натуральное число, то 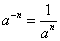. Степень с дробным показателем: полагают по определению, если 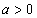и n - натуральное число, m - целое число, то .

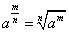Операции с корнями.

Во всех нижеприведенных формулах символ 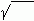означает арифметический корень (подкоренное выражение положительно).

1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:

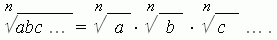
2. Корень из отношения равен отношению корней делимого и делителя:

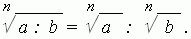
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число: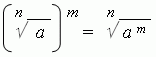

4. Если увеличить степень корня в n раз и одновременно возвести в n-ую степень подкоренное число, то значение корня не изменится: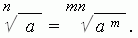

5. Если уменьшить степень корня в n раз и одновременно извлечь корень n-ой степени из подкоренного числа, то значение корня не изменится:

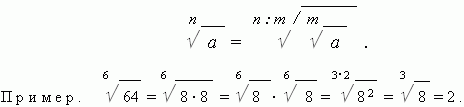
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.

Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя: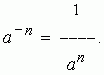

Теперь формула a ^m : a ⁿ = a ^{m - n} может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .

П р и м е р . a⁴ : a⁷ = a ^{4 - 7} = a ^-3 .

Если мы хотим, чтобы формула a ^m : a ⁿ = a ^{m - n} была справедлива при m = n , нам необходимо определение нулевой степени.

Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.

П р и м е р ы . 2 ⁰ = 1, ( – 5 ) ⁰ = 1, ( – 3 / 5 ) ⁰ = 1.

Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n–ой степени из m-ой степени этого числа а :

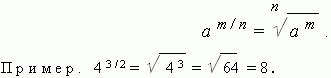
О выражениях, не имеющих смысла. Есть несколько таких выражений.

Случай 1.

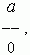где a ≠ 0 , не существует.

В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0

Случай 2.

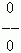- любое число.

В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.

Случай 3

Если считать, что правила действий со степенями распространяются и на степени с нулевым основанием, то 0 ⁰ - любое число.

Действительно,

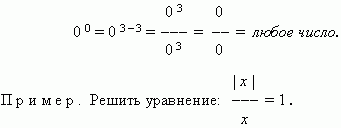
Р е ш е н и е . Рассмотрим три основных случая:

1) x = 0 – это значение не удовлетворяет данному уравнению

2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует, что x – любое число; но принимая во внимание, что внашем случае x > 0 , ответом является x > 0 ;

3) при x < 0 получаем: – x / x = 1, т.e. –1 = 1, следовательно,

в этом случае нет решения. Таким образом, x > 0.