Лекция 6. Показательная форма комплексного числа. Формула Эйлера.
Формы записи комплексного числа
Алгебраическая форма комплексного числа
Запись комплексного числа  в виде
в виде 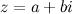 , где
, где  и
и 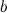 - действительные числа, называется алгебраической формойкомплексного числа.
- действительные числа, называется алгебраической формойкомплексного числа.
Например. 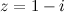
Тригонометрическая форма комплексного числа
Если 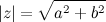 - модуль комплексного числа
- модуль комплексного числа 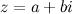 , а
, а 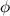 - его аргумент, то тригонометрической формойкомплексного числа
- его аргумент, то тригонометрической формойкомплексного числа  называется выражение
называется выражение
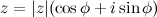
Задание. Записать число 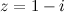 в тригонометрической форме.
в тригонометрической форме.
Решение. Для получения тригонометрической формы заданного комплексного числа найдем вначале его модуль и аргумент. Так как 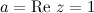 ,
, 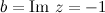 , то
, то
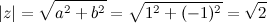
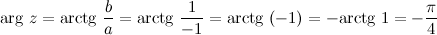
Тогда тригонометрическая форма заданного числа 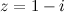 имеет вид:
имеет вид:
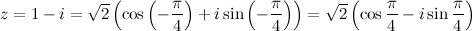
Ответ. 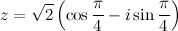
Показательная форма комплексного числа
Показательной формой комплексного числа 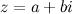 называется выражение
называется выражение
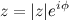
Задание. Комплексное число 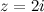 записать в показательной форме.
записать в показательной форме.
Решение. Найдем модуль и аргумент заданного комплексного числа:
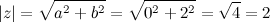
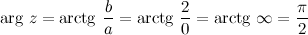
А тогда имеем, что
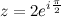
Ответ. 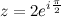
Заметим, что показательную и тригонометрическую формы комплексного числа связывает формула Эйлера:
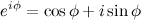
Дата добавления: 2016-06-05; просмотров: 2413;











