Обыкновенные линейные САУ

Как отмечалось выше, под действием управляющих и возмущающих воздействий в системе возникают динамические переходные процессы.

Динамика таких систем описывается дифференциальным уравнением вида:

(1)

Смысл этого уравнения:

Под действием, управляющего воздействия X и его m производных, а так же под действием возмущающего воздействия fи его производных происходит изменение регулируемой величины y и ее n производных.

Решение дифференциального уравнения (1) при заданных X , f и начальных условиях - есть переходный процесс в этой системе. Уравнение (1) может быть линейным с постоянными коэффициентами, линейным с переменными коэффициентами, нелинейным, содержать чистое (транспортное) запаздывание и т.д.

Каждый тип уравнения определяет класс САУ. Для каждого класса САУ разрабатываются свои методы исследования. Наиболее полной и простой является теория обыкновенных линейных систем. Вместе с тем с ее помощью можно решить большое количество практически важных задач.

Обыкновенными линейными системами, называются системы, динамические процессы в которых описываются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами и все статические характеристики элементов этой системы также линейны.

Статический характеристикой называется зависимость выходной величины от входной на установившемся режиме.

T2

Линейность статической характеристики понимается в ограниченном смысле. Если рассматривать широкий диапазон изменения входной величины, то статические характеристики большинства элементов будут нелинейными.

Uвых.

Если же входной сигнал изменяется в диапазоне от U₁ до U₂, то можно считать, что статическая характеристика линейна. Замена нелинейной характеристики линейной называется линеаризацией.

Динамика обыкновенных линейных систем в общем виде описывается дифференциальным уравнением вида:

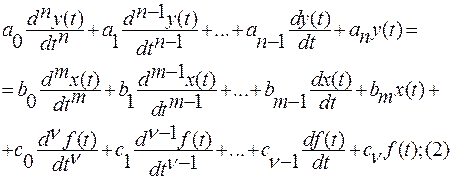
Смысл уравнения (2) такой же, как и уравнения (1).

Здесь - любые целые положительные числа, - постоянные коэффициенты.