ГЛАВА 2. НЕКОТОРЫЕ ЛИНЕЙНЫЕ ОБРАЗЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
§9. Теорема Дезарга
Теорема Дезарга детализирует свойства перспективного расположения трехвершинников. Жерар Дезарг (1593-1662) – французский математик, инженер и архитектор сформулировал свою замечательную теорему в 1636 году в работе, объемом в 12 страниц.
Трехвершинником называется фигура, составленная из трех точек, не лежащих на одной прямой (вершин треугольника), и трех прямых попарно соединяющих эти точки (сторон трехвершинника). (Двойственным понятием является трехсторонник, состоящий из трех прямых, не проходящих через одну точку – сторон и трех точек – вершин - попарных пересечений сторон). Говорят, что трехвершинники ABC и A¢B¢C¢ имеют центр перспективы Q, если вершины A и A¢, B и B¢, C и C¢ лежат на прямых, проходящих через одну точку Q. Трехвершинники ABC и A¢B¢C¢ имеют ось перспективы q, если стороны (АВ)и (A¢B¢), (BC) и (B¢C¢), (AC) и (A¢C¢) пересекаются в точках, лежащих на прямой q.
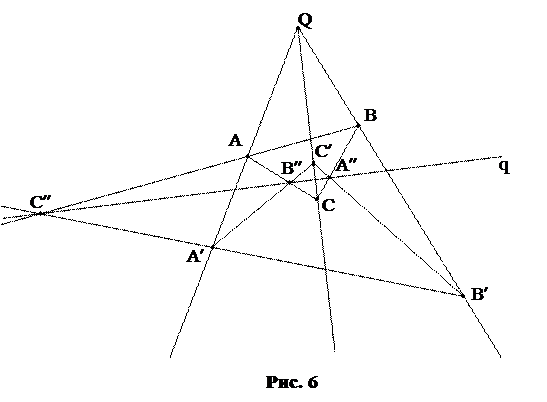 |
Теорема Дезарга. Трехвершинники имеют центр перспективы тогда и только тогда, когда они имеют ось перспективы.
Рассматривая рисунок 6, замечаем, что невырожденная конфигурация Дезарга состоит из десяти точек (A, B, C, A¢, B¢, C¢, A¢¢, B¢¢, C¢¢, Q) и десяти прямых ((AA¢), (BB¢), (CC¢), (AB), (AC), (BC), (A¢B¢), (A¢C¢), (B¢C¢), q).
Допустим, что трехвершинники ABC и A¢B¢C¢ лежат в одной проективной плоскости и имеют центр перспективы Q = (AA¢)  (BB¢)
(BB¢)  (CC¢). Используя метод проективных координат, докажем, что трехвершинники ABC и A¢B¢C¢ имеют ось перспективы q. В случае вырождения конфигурации, например, если точка Q лежит на одной из прямых (AB), (AC), (BC), или, если две какие-либо точки совпадают, то утверждение становится очевидным. Рассмотрим невырожденный случай. Пусть никакие три из четырех точек A, B, C, Q не лежат на одной прямой, тогда имеет место проективный репер Â = (A, B, C, Q). Введем в рассмотрение координаты точек A¢, B¢, C¢ в этом репере. Точка A¢ принадлежит прямой (QA). Точка Q – единичная точка репера Â, Q(1, 1, 1), точка A – первая точка репера, A(1, 0, 0). Составим уравнение прямой (QA):
(CC¢). Используя метод проективных координат, докажем, что трехвершинники ABC и A¢B¢C¢ имеют ось перспективы q. В случае вырождения конфигурации, например, если точка Q лежит на одной из прямых (AB), (AC), (BC), или, если две какие-либо точки совпадают, то утверждение становится очевидным. Рассмотрим невырожденный случай. Пусть никакие три из четырех точек A, B, C, Q не лежат на одной прямой, тогда имеет место проективный репер Â = (A, B, C, Q). Введем в рассмотрение координаты точек A¢, B¢, C¢ в этом репере. Точка A¢ принадлежит прямой (QA). Точка Q – единичная точка репера Â, Q(1, 1, 1), точка A – первая точка репера, A(1, 0, 0). Составим уравнение прямой (QA):
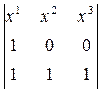 = –x2 + x3 = 0
= –x2 + x3 = 0
Если точка A¢ не совпадает с точкой A, то можно положить A¢(a, 1, 1), где a – некоторое действительное число. Аналогично обозначим B¢(1, b, 1), C¢(1, 1, c); b, c 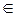 R. Заметим, что a
R. Заметим, что a  1, b
1, b 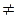 1, c
1, c 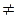 1, т.к. A¢
1, т.к. A¢ 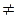 Q, B¢
Q, B¢ 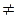 Q, C¢
Q, C¢ 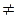 Q. Вычислим координаты точки C¢¢ = (AB)
Q. Вычислим координаты точки C¢¢ = (AB)  (A¢B¢). Прямая (AB) – третья координатная прямая, её уравнение: x3 = 0. Найдем уравнение прямой (A¢B¢):
(A¢B¢). Прямая (AB) – третья координатная прямая, её уравнение: x3 = 0. Найдем уравнение прямой (A¢B¢):
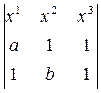 =x1
=x1 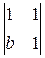 –x2
–x2 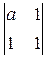 +x3
+x3 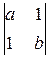 =(1–b)x1+(1–a)x2+(ab–1)x3=0
=(1–b)x1+(1–a)x2+(ab–1)x3=0
Рассмотрим однородную систему двух линейных уравнений с тремя неизвестными x1, x2, x3:
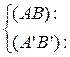
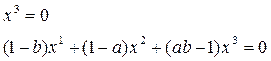
Система имеет бесконечное множество решений, например, один из возможных вариантов это – (1–a, b–1, 0). Можно указать все решения системы:
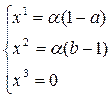 ,
, 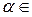 R
R
Поскольку координаты точки на проективной плоскости задаются с точностью до ненулевого сомножителя, то, без ограничения общности, полагаем 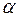 =1 и окончательно имеем C¢¢ = (1–a, b–1, 0). Аналогично B¢¢ = (1–a, 0, c–1), A¢¢ = (0, 1–b, c–1). Проверим, что точки A¢¢, B¢¢, C¢¢ принадлежат одной прямой. Для этого составим определитель из их координат:
=1 и окончательно имеем C¢¢ = (1–a, b–1, 0). Аналогично B¢¢ = (1–a, 0, c–1), A¢¢ = (0, 1–b, c–1). Проверим, что точки A¢¢, B¢¢, C¢¢ принадлежат одной прямой. Для этого составим определитель из их координат:
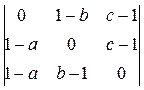 = – (1–b)
= – (1–b) 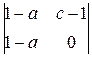 + (c–1)
+ (c–1) 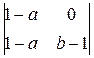 =
=
=(b–1)(1–a)(1–c)+(c–1)(1–a)(b–1)=0
Напомним, что три точки проективной плоскости лежат на одной прямой, тогда и только тогда, когда определитель, составленный из их координат, равен нулю.
Следовательно, точки A¢¢, B¢¢, C¢¢ принадлежат одной прямой, которая является осью перспективы. Мы доказали прямое утверждение Дезарга для проективной плоскости о том, что наличие центра перспективы влечет за собой существование оси перспективы. Обратное утверждение двойственно исходному по принципу двойственности для проективной плоскости.
Задача 20.Разместить на плоскости десять деревьев в десяти рядах по три в ряду.
Задача 21. На чертеже ограниченных размеров заданы точка А и пара прямых p и q, пересекающихся за пределами чертежа в недоступной точке В. Используя теорему Дезарга, построить доступную часть прямой (АВ).
Задача 22. С помощью одной линейки через данную точку А провести прямую, параллельную двум заданным не совпадающим прямым p и q.
Задача 23. Трапеция ABCD пересечена прямыми p и q, параллельными основанию [AB], p  (AD)=M, p
(AD)=M, p  (AC)=P, q
(AC)=P, q  (BD)=N, q
(BD)=N, q  (BC)=Q. Доказать, что точка (MN)
(BC)=Q. Доказать, что точка (MN)  (PQ) лежит на прямой (AB).
(PQ) лежит на прямой (AB).
 |
Задача 24.Внутри треугольникаАВС выбрана точка D и проведены прямые (AD), p и q, так что p||q||(AD), p
 (AB)=M, p
(AB)=M, p  (DB)=P, q
(DB)=P, q  (AC)=N, q
(AC)=N, q  (DC)=Q (см. рис.7). Доказать, что прямые (MN), (PQ) и (BC) принадлежат одному пучку.
(DC)=Q (см. рис.7). Доказать, что прямые (MN), (PQ) и (BC) принадлежат одному пучку.
Замечание. Проективную плоскость можно рассматривать над некоторым кольцом. (При этом необходимо дать «внутреннее» определение проективной плоскости, не вкладывая плоскость в трехмерное пространство).
Доказано [8], что при этом кольцо является телом тогда и только тогда, когда на проективной плоскости замыкается конфигурация Дезарга. Дезарговость проективной плоскости равносильна возможности её вложения в трехмерное пространство.
В дальнейшем мы рассмотрим конфигурацию Паппа, состоящую из 9 точек и 9 прямых. Если на проективной плоскости замыкается конфигурация Паппа, то замыкается и конфигурация Дезарга; обратное, вообще говоря, неверно, если мы рассматриваем проективную геометрию над телом. Если на проективной плоскости над телом замыкается конфигурация Паппа, то тело является полем.
Теорема Дезарга верна в случае, когда перспективные трехвершинники расположены в разных плоскостях трехмерного проективного пространства. Допустим, что трехвершинники ABC и A¢B¢C¢ имеют центр перспективы Q и расположены соответственно в плоскостях 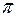 и
и 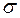 (рис. 8). Т.к. Q = (AA¢)
(рис. 8). Т.к. Q = (AA¢)  (BB¢), то точки A, B, A¢, B¢ лежат в одной плоскости, и прямые (AB) и (A¢B¢) имеют точку пересечения C¢¢, которая обязательно принадлежит прямой пересечения плоскостей
(BB¢), то точки A, B, A¢, B¢ лежат в одной плоскости, и прямые (AB) и (A¢B¢) имеют точку пересечения C¢¢, которая обязательно принадлежит прямой пересечения плоскостей 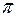 и
и 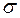 . Аналогично, ((AC)
. Аналогично, ((AC)  (A¢C¢))
(A¢C¢)) 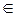
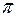

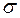 , ((BC)
, ((BC)  (B¢C¢))
(B¢C¢)) 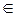
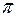

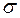 , и, следовательно,
, и, следовательно, 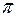

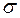 есть ось перспективы трехвершинников ABC и A¢B¢C¢. Обращая рассуждения, убеждаемся в обратном, т.е. если трехвершинники ABC и A¢B¢C¢, расположенные в разных плоскостях трехмерного проективного пространства имеют ось перспективы, то они
есть ось перспективы трехвершинников ABC и A¢B¢C¢. Обращая рассуждения, убеждаемся в обратном, т.е. если трехвершинники ABC и A¢B¢C¢, расположенные в разных плоскостях трехмерного проективного пространства имеют ось перспективы, то они
 |
имеют и центр перспективы.
Замечание. В трехмерном проективном пространстве прямая и обратная теоремы Дезарга не двойственны.
§10. Сложное отношение четырех точек прямой
Пусть на проективной прямой даны точки A, B, C, D. Поставим задачу сопоставления действительного числа упорядоченной четверке проективных точек. Если все четыре точки совпадают, то трудно ожидать решения проблемы, т.к. на проективной прямой все точки равноправны. Допустим A 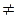 D, B
D, B 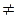 C, A
C, A 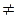 B.
B.  Если A=C, то будем считать, что сложное отношение (AB, CD) = 0. Если A
Если A=C, то будем считать, что сложное отношение (AB, CD) = 0. Если A 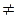 C, то точки A, B, C образуют проективный репер, в котором точка D(x1, x2) имеет определенные координаты. В этом случае положим (AB, CD)=
C, то точки A, B, C образуют проективный репер, в котором точка D(x1, x2) имеет определенные координаты. В этом случае положим (AB, CD)= 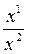 . Часто сложное отношение называют двойным или ангармоническим.
. Часто сложное отношение называют двойным или ангармоническим.
Легко понять, что если A, B, C – попарно различные точки, а t – любое действительное число, то на данной прямой существует одна и только одна точка D такая, что (AB, CD) = t. Если на прямой даны точки D и Е, так что (AB, CD) = (AB, CE), то D = E.
Следующая теорема показывает, как вычислять сложное отношение четырех точек по их координатам в проективном репере.
Теорема. Если точки A, B, C и D, лежащие на некоторой прямой, имеют в некотором проективном репере координаты A(a1, a2), B(b1, b2), C(c1, c2), D(d1, d2),причем A 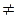 D, B
D, B 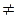 C, то
C, то
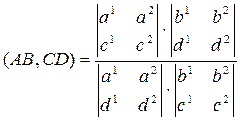 .
.
Приведем простейшие свойства сложного отношения четырех точек прямой.
1) (AB, CD) = (CD, AB)
2) (AB, CD) = 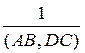 =
= 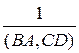 , если (AB, DC)
, если (AB, DC) 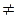 0
0
3) (AB, CD) = (BA, DC)
4) (AB, CC) = 1; (AB, CB) = 0
5) (AB, CD) + (AC, BD) = 1
Задача 25.Пусть A, B, C, D – четыре попарно различные точки на проективной прямой, сложное отношение которых (AB, CD) = t, где t – заданное число. Записать значения сложных отношений всех четверок точек, которые можно составить из точек A, B, C, D, переставляя их всеми возможными способами.
Задача 26. Доказать, что для пяти попарно различных точек A, B, C, D, E на проективной прямой имеет место равенство
(AB, CE) = (AB, CD)(AB, DE).
§11. Сложное отношение четырех прямых пучка проективной плоскости
Рассмотрим две прямые d и d¢ проективной плоскости и точку О, не принадлежащую этим прямым. Точку О примем за центр проекции. Для любой точки М на d поставим в соответствие точку M¢ на d¢: M¢ = d¢  (OM). Точка M¢ называется проекцией точки М из центра О, а само отображение называется проекцией.
(OM). Точка M¢ называется проекцией точки М из центра О, а само отображение называется проекцией.
Теорема. Проекция сохраняет сложное отношение четырех точек прямой.
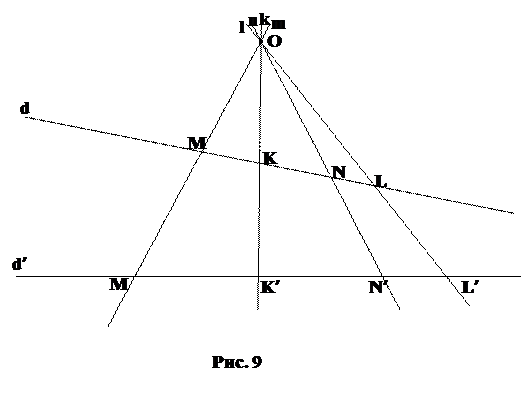 |
(MN, KL) = (M¢N¢,K¢L¢)
Определение.Если m, n, k, l – четыре прямые на проективной плоскости, проходящие через точку О, то их сложным отношением называется сложное отношение четырех точек, высекаемых на некоторой прямой d, не проходящей через точку О.
(mn, kl) = (MN, KL)
Замечание.Определение корректно, поскольку сложное отношение четырех прямых не зависит от выбора прямой d.
Определение.Пара прямых a и b гармонически разделяет пару прямых c и d, если (ab, cd) = –1.
Задача 27.Прямые a и b евклидовой плоскости пересекаются в точке О, прямые c и d содержат биссектрисы углов, образованных прямыми a и b. Доказать, что (ab, cd) = –1.
Задача 28.Доказать, что прямые, содержащие диагонали параллелограмма, гармонически разделяют прямые, проходящие через центр параллелограмма параллельно его сторонам.
Задача 28. Доказать, что прямая (CM), содержащая медиану [CM] треугольника АВС, и прямая (CX), параллельная стороне [AB], гармонически разделяют прямые (CA) и (CB), содержащие две другие стороны треугольника АВС.
§12. Полный четырехвершинник на проективной плоскости
Определение.Полным четырехвершинником называется фигура, состоящая из четырех точек – вершин проективной плоскости, никакие три из которых не лежат на одной прямой; и шести прямых – сторон, попарно соединяющих вершины.
Стороны, не имеющие общей вершины, называются противоположными. Точки пересечения противоположных сторон называются диагональными.
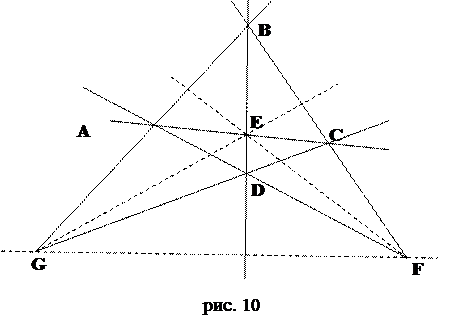 |
На рисунке 10 изображен четырехвершинник ABCD, где A, B, C, D – вершины; (AB) и (CD), (BC) и (AD), (BD) и (AC) – пары противоположных сторон; E, F, G – диагональные точки.
Можно легко доказать, что диагональные точки полного четырехвершинника не лежат на одной прямой.
Рассмотрим подробнее фигуру, определяемую полным четырехвершинником.
Прямые, попарно соединяющие диагональные точки, называются диагоналями. На рисунке 10 диагонали изображены пунктиром.
Следующая теорема показывает, что полный четырехвершинник содержит в себе гармонические четверки точек и прямых.
Теорема. На каждой диагонали полного четырехвершинника диагональные точки гармонически разделяют две точки, в которых эта диагональ пересекает стороны, проходящие через третью диагональную точку.
 |
(GF, KL) = –1.
Следствие 1. Две вершины, лежащие на стороне полного четырехвершинника, гармонически разделяют пару точек, состоящую из диагональной точки и точки, в которой эта сторона пересекает диагональ, проходящую через другие диагональные точки.
Следствие 2.Две противоположные стороны полного четырехвершинника гармонически разделяют две диагонали, проходящие через точку пересечения этих сторон.
Условимся называть точу Х четвертой гармонической к трем данным точкам А, В, С, если (АВ, СХ) = –1.
Задача 30.На аффинной (или евклидовой) плоскости задан отрезок [AB] и его середина С. Пользуясь только линейкой без делений, провести прямую через данную точку D, не принадлежащую прямой (АВ), параллельно этой прямой.
Задача 31.Даны две различные параллельные прямые. Пользуясь только линейкой, построить середину отрезка, заданного на одной из данных прямых.
Задача 32. На аффинной (евклидовой) плоскости задан параллелограмм (окружность с центром), прямая m и точка А. С помощью одной линейки через точку А провести прямую, параллельную прямой m.
Задача 33.Построить четвертую гармоническую точку Х к трем данным точкам А, В, С, лежащим на одной прямой.
§13. Проективные отображения прямых и пучков
Допустим, что две прямые g и g¢ принадлежат одной проективной плоскости. Взаимно однозначное отображение всех точек прямой g на множество точек прямой g¢ называется проективным, если оно сохраняет сложное отношение четырех точек.
Имеет место следующая теорема.
Теорема. Биекция f:g 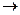 g¢ прямой g на прямую g¢ является проективным отображением, если и только если, каждый проективный репер  прямой g переходит в проективный репер ¢ прямой g¢ и выполняется правило равенства координат: прообраз – точка M(x1, x2) на прямой g имеет такие же координаты в репере Â, что и образ – точка M¢ (x1, x2) в репере ¢ на прямой g¢.
g¢ прямой g на прямую g¢ является проективным отображением, если и только если, каждый проективный репер  прямой g переходит в проективный репер ¢ прямой g¢ и выполняется правило равенства координат: прообраз – точка M(x1, x2) на прямой g имеет такие же координаты в репере Â, что и образ – точка M¢ (x1, x2) в репере ¢ на прямой g¢.
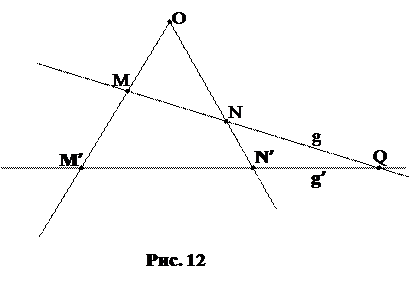 |
Примером проективного отображения одной прямой на другую служит перспектива. Пусть g и g¢ – две различные прямые проективной плоскости, и точка O, называемая центром перспективы, не лежит на этих прямых. Каждой точке M прямой g ставится в соответствие проекция M¢ на прямой g¢ из центра O.
Критерий перспективности. Для того, чтобы проективное отображение f:g  g¢ было перспективным, необходимо и достаточно, чтобы точка пересечения прямых g и g¢ переходила в себя.
g¢ было перспективным, необходимо и достаточно, чтобы точка пересечения прямых g и g¢ переходила в себя.
Теорема. Проективное отображение одной прямой на другую есть композиция не более двух перспектив.
Приведем иллюстрацию к этой теореме.
Задача 34. В проективном отображении f:g  g¢ репер Â=(A, B, C) переходит в репер ¢=(A¢, B¢, C¢). Построить образ произвольной точки M прямой g.
g¢ репер Â=(A, B, C) переходит в репер ¢=(A¢, B¢, C¢). Построить образ произвольной точки M прямой g.
Решение.
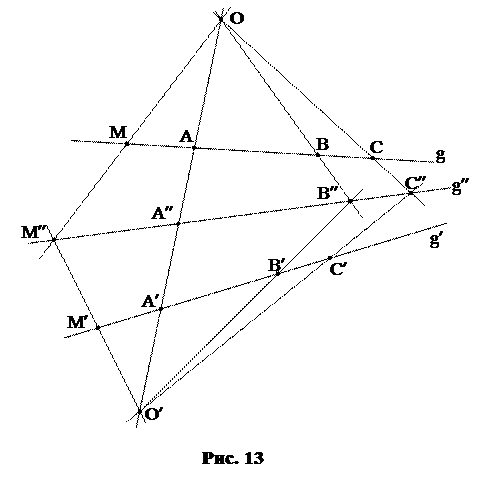 |
Проведем прямую (AA¢) и отложим на ней два центра перспективы O и O¢, отличные от точек A и A¢. Пусть B¢¢=(OB)
 (O¢B¢), C¢¢=(OC)
(O¢B¢), C¢¢=(OC)  (O¢C¢), g¢¢=(B¢¢, C¢¢), A¢¢=(OO¢)
(O¢C¢), g¢¢=(B¢¢, C¢¢), A¢¢=(OO¢)  g¢¢. Тогда перспектива fO с центром в точке O переводит репер  в репер ¢¢=(A¢¢, B¢¢, C¢¢) на прямой g¢¢, а перспектива fO¢ с центром в точке O¢ переводит репер ¢¢ в репер ¢, таким образом f=fO¢
g¢¢. Тогда перспектива fO с центром в точке O переводит репер  в репер ¢¢=(A¢¢, B¢¢, C¢¢) на прямой g¢¢, а перспектива fO¢ с центром в точке O¢ переводит репер ¢¢ в репер ¢, таким образом f=fO¢  fO. Далее находим точку M¢¢ на прямой g¢¢: M¢¢=(OM)
fO. Далее находим точку M¢¢ на прямой g¢¢: M¢¢=(OM)  g¢¢, и, наконец, M¢=(O¢M¢¢)
g¢¢, и, наконец, M¢=(O¢M¢¢)  g¢.
g¢.
Теорема. Проективное преобразование прямой на себя есть композиция не более трех перспектив.
Задача 35. В проективном преобразовании f:g  g прямой g на себя заданный репер Â=(A, B, C) переходит в заданный репер ¢=(A¢, B¢, C¢). Построить образ и прообраз произвольной данной точки M на g.
g прямой g на себя заданный репер Â=(A, B, C) переходит в заданный репер ¢=(A¢, B¢, C¢). Построить образ и прообраз произвольной данной точки M на g.
Двойственным образом строится теория проективных отображений пучков прямых на проективной плоскости.
Определение. Взаимно однозначное отображение пучка на пучёк называется проективным, если оно сохраняет сложное отношение четырех прямых.
Теорема. Если a, b, c – три произвольные прямые пучка с центром в точке O и a¢, b¢, c¢ – три произвольные прямые пучка с центром в точке O¢, то существует одно и только одно проективное отображение пучка O на пучок O¢, переводящее прямые a, b, c в прямые a¢, b¢, c¢.
 |
Рассмотрим пучки с центрами в двух точках O и O¢ и прямую d, не проходящую через точки O и O¢. Каждой прямой a пучка O поставим в соответствие прямую a¢ пучка O¢, которая проходит через точку пересечения прямых a и d.
Построенное отображение является проективным и называется перспективным. Прямая d называется осью перспективы.
Критерий перспективности. Для того, чтобы данное проективное отображение пучка на пучок было перспективным, необходимо и достаточно, чтобы прямая, проходящая через центры пучков, переходила в себя.
Задача 36. В проективном отображении f пучка O на пучок O¢ три попарно различные прямые a, b, c переходят соответственно в прямые a¢, b¢, c¢. Построить образ произвольной прямой m пучка O.
Решение.
Через точку A пересечения прямых a и a¢ проведем две прямые d и d¢, отличные от прямых a и a¢, и обозначим через B и C точки пересечения прямых b и c с прямой d, а через B¢ и C¢ точки пересечения прямых b¢ и c¢ с прямой d¢. Отображение f порождает перспективу прямой d на прямую d¢ с центром в точке S=(BB¢)  (CC¢).
(CC¢).
 |
Для построения образа произвольной прямой m находим сначала точку М, как пересечение прямых m и d, далее строим M¢=(SM)
 d¢. Прямая (O¢M¢) – искомая.
d¢. Прямая (O¢M¢) – искомая.
§14. Теорема Паппа
Рассмотрим одну из замечательных конфигураций действительной проективной геометрии. (Автором первой фундаментальной теоремы проективной геометрии является Папп Александрийский. Теорема Паппа содержится в «Математическом собрании», начало 1V века нашей эры)
Теорема. Пусть даны три точки A, B, C, лежащие на одной прямой d и три точки A¢, B¢, C¢, лежащие на прямой d¢, причем d  d¢. Тогда три точки A¢¢=(BC¢)
d¢. Тогда три точки A¢¢=(BC¢)  (B¢C), B¢¢=(A¢C)
(B¢C), B¢¢=(A¢C)  (C¢A), C¢¢=(AB¢)
(C¢A), C¢¢=(AB¢)  (A¢B) принадлежат одной прямой d¢¢.
(A¢B) принадлежат одной прямой d¢¢.
 |
Доказательство. Рассмотрим отображение f пучка прямых с центром в точке A на пучок прямых с центром в точке C, при котором прямые (AC), (AA¢), (AB¢) переходят, соответственно, в прямые (CA), (CA¢), (CB¢). Поскольку прямая, соединяющая центры пучков, переходит в себя, то f – перспективное отображение. Оно индуцирует перспективное отображение
 :(BA¢)
:(BA¢)  (BC¢) с центром B¢¢, при этом
(BC¢) с центром B¢¢, при этом 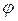 (С¢¢)=A¢¢. Значит, точка B¢¢ принадлежит прямой (A¢¢C¢¢).
(С¢¢)=A¢¢. Значит, точка B¢¢ принадлежит прямой (A¢¢C¢¢).
Задача 37.Посадить 9 деревьев так, чтобы получилось 10 рядов по три дерева в каждом.
Задача 38.Сформулируйте предложение, двойственное теореме Паппа. Сделать чертеж.
§15. Преобразования проективной прямой. Инволюции.
В геометрии принято определение, согласно которому термин «преобразование» обозначает «биекция» или «взаимно однозначное отображение» некоторого множества на себя.
Определение.Преобразование проективной прямой называется проективным, если оно сохраняет сложное отношение четырех точек.
Теорема. Проективное преобразование прямой d переводит проективный репер  на d в проективный репер ¢,и выполняется правило равенства координат, т.е. точка M 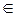 d имеет в репере  те же самые координаты, что и ее образ М¢ в репере ¢: M(x1, x2) в  и M¢ (x1, x2) в репере ¢.
d имеет в репере  те же самые координаты, что и ее образ М¢ в репере ¢: M(x1, x2) в  и M¢ (x1, x2) в репере ¢.
Замечание. Координаты точки в проективном пространстве задаются с точностью до ненулевого множителя.
Доказательство. Пусть на прямой d заданы проективное преобразование f: d 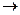 d и произвольный репер Â=(A, B, E).
d и произвольный репер Â=(A, B, E).
Пусть A¢= f(А), В¢= f(B), Е¢ = f(Е)). Поскольку f – биекция, то никакие две из трех точек A¢, В¢, Е¢ не совпадают, точки А¢, В¢, Е¢ занимают общее положение и образуют репер ¢=(A¢, B¢, E¢). Для произвольной точки М на d, М≠А определяются координаты (x1, x2) в репере Â, причем можно вычислить сложное отношение (А В, Е М) = 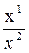 . Пусть М¢ = f(М), тогда (АВ, ЕМ) = (А¢В¢, Е¢М¢) по определениюпроективного преобразования, и (АВ, ЕМ) = (А¢В¢, Е¢М¢) =
. Пусть М¢ = f(М), тогда (АВ, ЕМ) = (А¢В¢, Е¢М¢) по определениюпроективного преобразования, и (АВ, ЕМ) = (А¢В¢, Е¢М¢) = 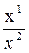 , и точка М¢ имеет в репере ¢ координаты(x1, x2).
, и точка М¢ имеет в репере ¢ координаты(x1, x2).
Следствие 1. Если  и ¢ - произвольные реперы на проективной прямой d, то существует единственное проективное преобразование на d, которое репер  переводит в репер ¢.
Следствие 2. Если проективное преобразование прямой имеет три попарно различные неподвижные (инвариантные) точки, то оно является тождественным преобразованием.
Задача 39. При проективном преобразовании f расширенной прямой 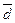 заданный репер  = (A, B, E) переходит в заданный репер ¢ = (A¢, B¢, E¢). Построить образ произвольной точки М прямой
заданный репер  = (A, B, E) переходит в заданный репер ¢ = (A¢, B¢, E¢). Построить образ произвольной точки М прямой 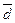 .
.
Задача 40. Доказать, что если в проективном преобразовании f расширенной прямой 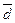 несобственная точка X∞
несобственная точка X∞ 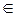
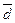 инвариантна, то сужение отображения f на аффинную прямую d =
инвариантна, то сужение отображения f на аффинную прямую d = 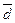 \{X∞}. f1d есть аффинное преобразование
\{X∞}. f1d есть аффинное преобразование
Определение. Нетождественное проективное преобразование прямой называется инволюцией, если оно совпадает со своим обратным преобразованием.
Теорема. Если в данном проективном преобразовании f прямой какая-то точка А переходит в точку В, отличную от точки А, а точка В переходит в точку А, то f – инволюция.
Доказательство. Пусть М – произвольная точка прямой, М¢ = f(М). Требуется доказать, что М = f(М¢). Обозначаем М¢¢ = f(М¢). При проективном преобразовании сохраняется сложное отношение четырех точек, следовательно, (АВ, М M¢) = (ВА, М¢M¢¢). Таким образом, по свойствам сложного отношения четырех точек прямой М = M¢¢.
Задача 41.Доказать, что инволюция прямой либо не имеет ни одной инвариантной точки, либо имеет две инвариантные точки.
§16. Преобразования проективной плоскости. Гомологии.
Определение. Преобразование проективной плоскости называется проективным, если точкам любой прямой соответствуют точки также лежащие на некоторой прямой.
Теорема. Проективное преобразование сохраняет сложное отношение четырех точек прямой.
Теорема. Пусть  и ¢ – произвольные реперы проективной плоскости. Тогда существует одно и только одно проективное преобразование, которое переводит репер  в репер ¢, при этом точка с данными координатами в репере  переходит в точку с теми же координатами в репере ¢.
Следствие. Если проективное преобразование имеет четыре инвариантные точки, из которых ни какие три не лежат на одной прямой, то оно является тождественным преобразованием.
Свойства проективных преобразований:
1. При проективном преобразовании три точки, не лежащие на одной прямой, переходят в три точки, также не лежащие на одной прямой.
2. При проективном преобразовании любой репер переходит в репер.
3. Проективное преобразование отображает прямую на прямую.
4. Проективное преобразование пучок прямых переводит в пучок прямых.
Теорема.Любое проективное преобразование плоскости имеет по крайней мере одну инвариантную точку и одну инвариантную прямую, которая не обязательно состоит из неподвижных точек.
Определение. Нетождественное проективное преобразование называется гомологией, если оно имеет, по крайней мере, три инвариантные точки, лежащие на одной прямой.
Можно легко доказать, что если точки A, В, и C, лежащие на одной прямой, являются неподвижными точками гомологии f, то все точки прямой (АВ) также являются инвариантными точками этой гомологии. Пусть М 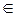 (АВ), М¢ = f(М), тогда (АВ, СМ) = (АВ, СМ¢), поэтому М = M¢.
(АВ), М¢ = f(М), тогда (АВ, СМ) = (АВ, СМ¢), поэтому М = M¢.
Прямая инвариантных точек называется осью гомологии.
Гомология имеет прямую инвариантных точек, и по принципу двойственности у гомологии существует пучок инвариантных прямых, проходящих через одну неподвижную точку, называемую центром гомологии. Гомология называется особой, если ее центр принадлежит оси и неособой в противном случае.
Таким образом, если S – центр, s – ось гомологии f, точка и точка M проективной плоскости не совпадает с центром, то S, M, f(M) коллинеарны, то есть принадлежат одной прямой. Если прямая d пересекает ось в некоторой точке D, то D – инвариантная точка, и D лежит на d¢ = f(d).
Теорема. Если на плоскости даны прямая s и три попарно различные точки S, A, A¢, лежащие на одной прямой, причем ни одна из точек A и A¢ не лежит на прямой s, то существует единственная гомологияf с осью s и центром S и такая, что f(A) = A¢.
Задача 42. Построить образ произвольной точки (прямой) на расширенной плоскости при действии гомологии f, если заданы центр S и ось гомологии, точка A и ее образ A¢ = f(A). ( Точки S, А и A¢ принадлежат одной прямой).
- “Что такое окружность?”
- “Это проективная прямая”
- “Что такое эллипс?”
- “Это искаженная окружность”
- “Что такое овал?”
- “Это обобщенный эллипс”
Из диалогов студентов.
Дата добавления: 2021-12-14; просмотров: 815;











