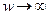Частотные критерии устойчивости.
В основе частотных критериев устойчивости лежит принцип аргумента, известный в теории функции комплексной переменной.
Принцип аргумента.
Дано характерное уравнение.
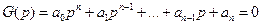
Пусть 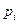 - корни характеристического уравнения,
- корни характеристического уравнения, 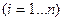
По основной теореме алгебры ( теореме Виетта) можем записать.
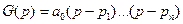
То есть характеристическое уравнение есть произведение элементарных сомножителей, где 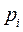 - корни характеристического уравнения.
- корни характеристического уравнения.
На комплексной плоскости корней каждому корню 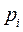 соответствует вполне определенная точка. Геометрически каждый корень
соответствует вполне определенная точка. Геометрически каждый корень 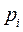 может быть изображен в виде вектора, проведенного из начала координат к точке
может быть изображен в виде вектора, проведенного из начала координат к точке 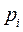 .
.
Длина вектора равна модулю комплексного числа, а угол, образованный вектором с положительным направлением действительной оси – аргумент или фаза комплексного числа 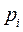 , т.е.
, т.е. 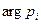 .
.

Сомножители 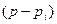 , входящие в
, входящие в 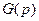 , геометрически изображаются векторами, проведенными из точки
, геометрически изображаются векторами, проведенными из точки 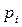 в точку
в точку 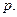 Каждый из этих векторов представляет собой разность двух векторов
Каждый из этих векторов представляет собой разность двух векторов 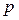 и
и 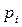 .
.
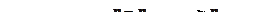

Длина 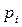
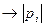 равна
равна 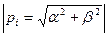
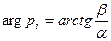
Пусть 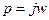 (уравнение мнимой оси). Тогда вектор характеристического уравнения примет вид.
(уравнение мнимой оси). Тогда вектор характеристического уравнения примет вид.
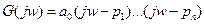
Концы каждого вектора 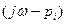 будут находиться на мнимой оси.
будут находиться на мнимой оси.
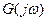 представляет собой произведение элементарных векторов.
представляет собой произведение элементарных векторов.
Из теории функции комплексной переменной известно, что длина такого вектора равна произведению длин элементарных векторов, а аргумента (угол поворота вектора характеристического уравнения при изменении частоты от минус бесконечности до плюс бесконечности)
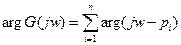
Найдем
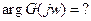 при изменении
при изменении 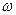 от -
от - 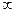 до +
до + 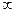 .
.
Считается поворот против часовой стрелки – положительным, а по часовой стрелке – отрицательным.
Пусть в системе 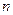 -го порядка имеется
-го порядка имеется 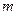 – правых корней и
– правых корней и 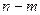 левых корней.
левых корней.
|


Если корень 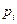 находится в левой полуплоскости, то при изменении
находится в левой полуплоскости, то при изменении 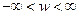 .
. 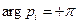
Если корень 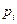 находится в правой полуплоскости, то при изменении
находится в правой полуплоскости, то при изменении 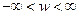 ,то
,то
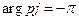
| |
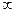 <
< 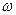 +
+ 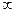
 угол поворота вектора характеристического уравнения
угол поворота вектора характеристического уравнения
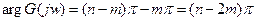
Принцип аргумента: Угол поворота вектора характеристического уравнения при изменении 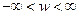 равен
равен 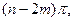 где
где 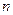 - порядок характеристического уравнения, а
- порядок характеристического уравнения, а 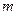 - количество правых корней.
- количество правых корней.
Для устойчивых САУ 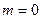 , и тогда
, и тогда 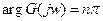
Дата добавления: 2019-09-30; просмотров: 639;