Способы соединения типовых элементарных звеньев (ТЭЗ)

1. Последовательное соединение

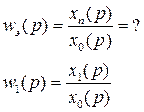
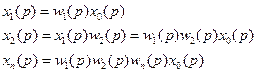
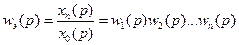
Передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев.

Пример.

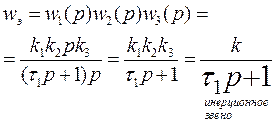
2. Параллельное соединение.

+

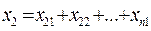
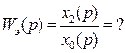
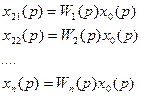
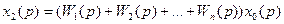
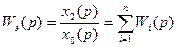
6.12.Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций этих звеньев.

Пример.

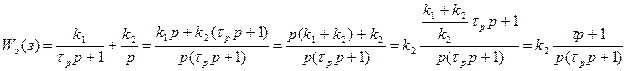
В результате параллельного соединения инерционного и интегрирующего звеньев получили дифференцирующее звено, интегрирующее и инерционное звенья. Т.о. не осуществляя операции дифференцирования с помощью дифференцирующей цепочки (эта операция плоха тем, что при дифференцировании вместе с полезным сигналом дифференцируются и помехи) получили эффект дифференцирования.

3. Соединение обратной связью

Это такое соединение, когда часть выходного сигнала через элемент обратной связи подается на вход системы.

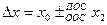
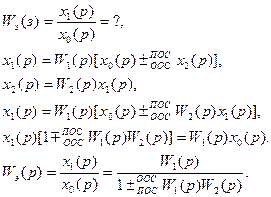
Передаточная функция звена, охваченного обратной связью, равна дроби, в числителе которой состоит передаточная функция прямой цепи, а в знаменателе 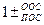произведение передаточной функции прямой и обратной цепей.

Пример:

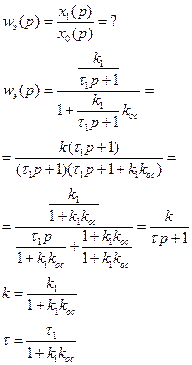
Инерционное звено охвачено жесткой отрицательной обратной связью. В результате получается тоже инерционное звено, меняются только параметры. Коэффициент усиления и постоянная времени уменьшаются в ( 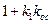)раз.

Получение передаточной функции замкнутой системы по управляющему и возмущающему воздействиям.

Мы рассмотрим линейные системы, к которым применим принцип суперпозиции. Это значит, что реакция системы на сумму воздействий, равна сумме реакций системы на каждое воздействие.

Поэтому при получении передаточной функции по управляющему воздействию положим 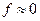, а по возмущающему воздействию -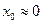

Получение передаточной функции по управляющему воздействию

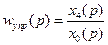
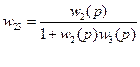
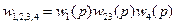
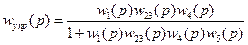
Получение передаточной функции по возмущающему воздействию.

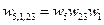
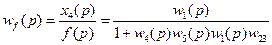
Обратите внимание: если выход один и тот же, то знаменатели передаточных функций по управляющему и по возмущающему воздействиям

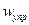( и 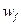) одинаковы.

Общее правило записи передаточной функции замкнутой системы по любому из приложенных воздействий.

Передаточная функция замкнутая по любому из приложенных воздей-

ствию равна дроби, в числителе которой стоит передаточная функция цепочки от места приложения воздействия до выхода, а в знаменателе

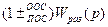, где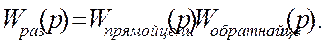

В домашней работе передаточные функции по управляющему и возмущающему воздействиям привести к виду:

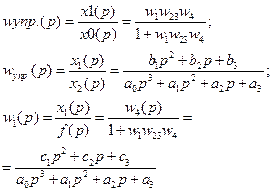
Лекция 7

Устойчивость САУ.

Устойчивость -это способность системы возвращаться к номинальному режиму после снятия возмущения , если она отклонилась по каким-то причинам от этого режима.

Требования к устойчивости обязательно для всех САУ.

Строгое определение устойчивости дано А.М. Ляпуновым в работе «Общая задача об устойчивости движения» (конец 19 века)

Пусть динамика системы описывается уравнением

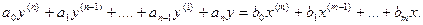(1)

y - выходная величина

x - входная величина

y⁽ⁱ⁾ , x^(j) - производные.

Предположим, что в этой системе существует номинальный режим работы у_н (t), который однозначно определяется номинальным входным воздействием х_н(t) и номинальными начальными условиями.

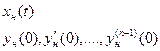(2)

Так как номинальные начальные условия (2) на практике трудно выдержать, в системе существует «отклоненные» начальные условия.

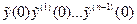(3)

Для номинального режима справедливо уравнение:

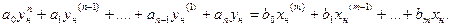(4)

Отклоненным начальным условиям соответствует отклоненный режим.

Для отклоненного режима справедливо уравнение:

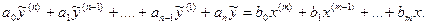(5)

Положим

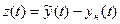(6)

Вычтем из уравнения (5) уравнение (4), получим 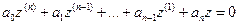(7)

Введем определение.

Номинальный режим у_н(t) устойчив по Ляпунову, если при любых отклоненных начальных условиях (3) , достаточно мало отличающихся от номинальных номинальных начальных условий (2), при всех t > 0 будет мало z(t).

Если номинальный режим устойчив по Ляпунову и при этом предел 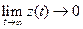, то номинальный режим называется асимптотически устойчивым.

Если найдутся начальные условия (3), сколько угодно мало отличающиеся от номинальных начальных условий (2), и при этом 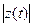станет больше некоторой малой, наперед заданной величины, то номинальный режим у_н(t) называется неустойчивым.

Из (7) следует, что поведение z(t) совершенно не зависит от вида входного воздействия х_н(t).

Отсюда следует вывод: либо в системе (1) асимптотически устойчивы все номинальные режимы, соответствующие разным входным х_н (t), либо они все неустойчивы.

Поэтому можно говорить об устойчивости или неустойчивости системы, а не какого-либо одного ее режима.

Это важный вывод, сокращающий объем исследований САУ.

К сожалению, он справедлив только для линейных САУ.