Критерий устойчивости Михайлова.
Критерий устойчивости Михайлова является геометрической интерпретацией принципа аргумента. При изменении частоты 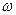 от
от 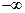 до
до 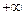 конец вектора характеристического уравнения на комплексной плоскости описывает кривую, которая называется характеристической кривой или годографом Михайлова. Для того, чтобы получить уравнение годографа Михайлова, надо в характеристическое уравнение подставить
конец вектора характеристического уравнения на комплексной плоскости описывает кривую, которая называется характеристической кривой или годографом Михайлова. Для того, чтобы получить уравнение годографа Михайлова, надо в характеристическое уравнение подставить 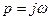
и выделить вещественную и мнимую части.
Пусть характеристическое уравнение.
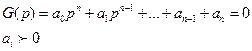
Подставим 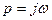
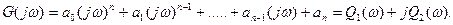
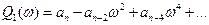
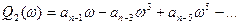
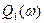 - является четной функции частоты ,т.е
- является четной функции частоты ,т.е 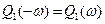 .
. 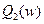 - является нечетной функцией частоты ,т.е.
- является нечетной функцией частоты ,т.е. 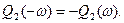 Таким образом, годограф будет симметричен относительно вещественной оси.
Таким образом, годограф будет симметричен относительно вещественной оси.

Это означает что при его построении достаточно менять частоту 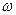 от 0 до
от 0 до 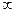 . При этом аргумент
. При этом аргумент 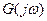 (угол поворота вектора характеристического уравнения) уменьшается в 2 раза и для устойчивой системы он будет равен
(угол поворота вектора характеристического уравнения) уменьшается в 2 раза и для устойчивой системы он будет равен 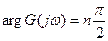 . То есть годограф Михайлова устойчивой системы должен проходить
. То есть годограф Михайлова устойчивой системы должен проходить 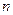 квадрантов.
квадрантов.
САУ устойчивая, если при 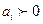 , годограф Михайлова начинается на положительной части действительной оси и обходит в положительном направлении, то есть против часовой стрелки, последовательно
, годограф Михайлова начинается на положительной части действительной оси и обходит в положительном направлении, то есть против часовой стрелки, последовательно 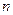 квадрантов
квадрантов

Годограф начинается со свободного члена характеристического уравнения.
Если годографы соответствуют устойчивым системам, то это означает, что корни характеристического уравнения расположены в левой полуплоскости комплексной плоскости корней.
Если годограф Михайлова проходит через начало координат , то САУ находится на границе устойчивости и хотя бы один корень расположен на мнимой оси.
Критерий устойчивости Найквиста.
Все рассмотренные выше критерии устойчивости позволяют определить устойчивость замкнутой системы по характеристическому уравнению замкнутой системы.
Критерий устойчивости Найквиста позволяет по поведению амплитудно-частотной характеристики разомкнутой системы, определить устойчивость замкнутой системы, если она замкнута единичной отрицательной обратной связью. Этот критерий удобен тем, что АФЧХ разомкнутой системы может быть получена экспериментально. Хотя АФЧХ может быть рассчитана и теоретически.
Пусть имеем замкнутую систему с единичной отрицательной обратной свяэью.

Пусть
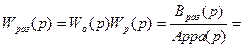
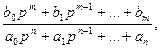
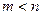
Будем считать, что разомкнутая система устойчива.
Передаточная функция замкнутой системы
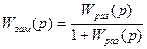 .
.
Рассмотрим характеристическое уравнение замкнутой системы
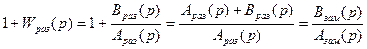
Подставим сюда 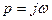 и применим принцип аргумента
и применим принцип аргумента
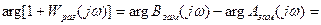
Порядок 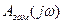 равен порядку
равен порядку 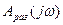 и равен
и равен 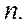 Следовательно,
Следовательно,
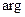
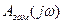 =
= 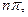 т.к
т.к 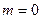 (по условию, что разомкнутая система устойчива, следовательно
(по условию, что разомкнутая система устойчива, следовательно 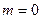 )
)
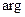
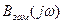 определяется полиномом
определяется полиномом 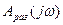 +
+ 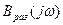 . Порядок полинома
. Порядок полинома 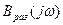 меньше порядка полинома
меньше порядка полинома 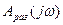 . Поэтому порядок
. Поэтому порядок 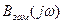 имеет порядок
имеет порядок 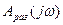 , т.е
, т.е 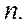 Поэтому
Поэтому 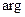
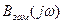 =
= 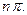 И
И 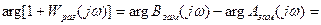
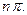 -
- 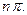 =0
=0
Если изобразить на комплексной плоскости годограф 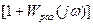 , то вектор
, то вектор 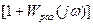 при возрастании
при возрастании 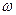 от
от 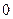 до +
до + 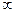 должен в сумме описать угол, равный нулю. Это будет лишь в том случае, когда этот годограф не будет охватывать начало координат. Изобразим этот годограф при изменении
должен в сумме описать угол, равный нулю. Это будет лишь в том случае, когда этот годограф не будет охватывать начало координат. Изобразим этот годограф при изменении 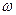 от
от 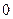 до +
до + 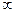

От годографа 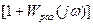 можно перейти к годографу
можно перейти к годографу 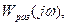 т.е. к АФЧХ разомкнутой системы, которая представляет собой ту же кривую, но сдвинутую на 1 влево( тот же результат можно получить, если сдвинуть мнимую ось на 1 вправо)
т.е. к АФЧХ разомкнутой системы, которая представляет собой ту же кривую, но сдвинутую на 1 влево( тот же результат можно получить, если сдвинуть мнимую ось на 1 вправо)

Критерий устойчивости Найквиста
1.Пусть разомкнутая система асимптотически устойчива, тогда для устойчивости системы , замкнутой единичной обратной связью, необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывало точку с координатами 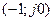
|

2.Пусть разомкнутая система неустойчива и ее характеристическое уравнение имеет m правых корней. Тогда для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы огибала точку (-1,j0) 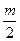 раз в положительном направлении (если m нечетная, то
раз в положительном направлении (если m нечетная, то 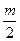 дробь. Это означает, что АФЧХ начинается левее точки (-1,j0)
дробь. Это означает, что АФЧХ начинается левее точки (-1,j0)
(0,5 раза) и один раз пересекает ее.
Примеры
 Система устойчива в разомкнутом и в замкнутом состояниях
Система устойчива в разомкнутом и в замкнутом состояниях

Система устойчива в разомкнутом состоянии и неустойчива в замкнутом.

Система неустойчива в разомкнутом и устойчива в замкнутом состояниях.
Этот критерий удобен еще и тем, что устойчивость разомкнутой системы легко определить.
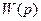 разомкнутой системы есть произведения
разомкнутой системы есть произведения 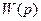 - передаточных функций элементов САУ не выше второго порядка , включенных последовательно. Поэтому устойчивость разомкнутой системы определить просто – надо найти корни сомножителей знаменателя передаточной функции разомкнутой системы (это просто, т.к. это уравнения первого или второго порядка)
- передаточных функций элементов САУ не выше второго порядка , включенных последовательно. Поэтому устойчивость разомкнутой системы определить просто – надо найти корни сомножителей знаменателя передаточной функции разомкнутой системы (это просто, т.к. это уравнения первого или второго порядка)
Этот прием нельзя применять для замкнутых систем.
Лекция 8
Построение границы области устойчивости в пространстве параметров САУ
(D-разбиение пространства параметров САУ)
В процессе эксплуатации САУ параметры объекта регулирования и регулятора могут изменяться, а, следовательно, изменяются и динамические свойства замкнутой САУ. Кроме того, ряд таких параметров как запаздывание в системе вообще бывает оценить трудно. Поэтому для разработчика САУ важно знать, как далеко находится система от границы области устойчивости или иначе каков запас устойчивости.
Для этой цели представляет интерес нанести в пространстве параметров границу устойчивости данной системы. Такими параметрами могут быть, например, коэффициент усиления 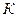 и постоянная времени
и постоянная времени 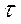
Построение области устойчивости можно производить ,в принципе, любым из рассмотренных выше критериев устойчивости, проведя ряд построений при различных сочетаниях параметров. Можно также получить уравнение границы устойчивости из критерия Гурвица. Однако уже при 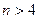 возникают значительные трудности при непосредственном определении границы устойчивости по этим критериям.
возникают значительные трудности при непосредственном определении границы устойчивости по этим критериям.
Неймарком в 1948 году был предложен метод выделения устойчивости в плоскости параметров системы – метод Д- разбиения.
Выделим в плоскости параметров А1 –А2 системы области с одинаковым расположением корней характеристического уравнения.
 Область
Область 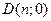 - n - «левых» корней
- n - «левых» корней
0 - «правых» корней
Область 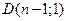 имеет n-1 левых и один правый корень
имеет n-1 левых и один правый корень
Область 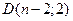 имеет n-2 левых и 2 правых корней
имеет n-2 левых и 2 правых корней
Разбиение плоскости (пространства) на области с одинаковыми индексами называется D-разбиением плоскости (пространства) параметров.
Среди выделенных областей нас интересует область устойчивости, т.е. область 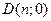 . Границей области устойчивости является мнимая ось. Таким образом, границу области
. Границей области устойчивости является мнимая ось. Таким образом, границу области 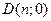 можно рассматривать как проекцию мнимой оси на плоскость параметров системы.
можно рассматривать как проекцию мнимой оси на плоскость параметров системы.
Система будет находиться на границе устойчивости, если хотя бы один ее корень расположен на мнимой оси. Уравнение корня, лежащего на мнимой оси, 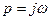 .
.
Подставив этот корень в характеристическое уравнение, мы можем для каждой 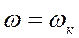 найти такие значения коэффициентов характеристического уравнения, при которых это характеристическое уравнение обращается в ноль. Эти коэффициенты определяют в плоскости параметров системы точку, лежащую на границе устойчивости, т.е. на границе D-разбиения. Можно сказать, что граница D-разбиения является проекцией мнимой оси на плоскость параметров системы.
найти такие значения коэффициентов характеристического уравнения, при которых это характеристическое уравнение обращается в ноль. Эти коэффициенты определяют в плоскости параметров системы точку, лежащую на границе устойчивости, т.е. на границе D-разбиения. Можно сказать, что граница D-разбиения является проекцией мнимой оси на плоскость параметров системы.
Таким образом, изменяя 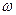 от
от 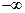 до
до 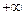 можно выделить границу устойчивости системы. Однако выделенная область будет областью с минимальным количеством правых корней. Для того чтобы убедится, что она будет областью устойчивости, нужно взять любую точку из этой области, подставить ее координаты в характеристическое уравнение и проверить полученное характеристическое уравнение на устойчивость. Если окажется, что в этой точке САУ устойчива, следовательно, вся выделенная область является областью устойчивости.
можно выделить границу устойчивости системы. Однако выделенная область будет областью с минимальным количеством правых корней. Для того чтобы убедится, что она будет областью устойчивости, нужно взять любую точку из этой области, подставить ее координаты в характеристическое уравнение и проверить полученное характеристическое уравнение на устойчивость. Если окажется, что в этой точке САУ устойчива, следовательно, вся выделенная область является областью устойчивости.
D – разбиение проводится в плоскости одного, двух или в пространстве параметров.
Выделение области устойчивости в плоскости коэффициента усиления системы.
Коэффициент усиления K- один из наиболее важных параметров системы. От него в значительной степени зависит устойчивость системы и качество процессов управления.
Для того, чтобы выделить область устойчивости в плоскости К нужно в характеристическом уравнении выделить члены, содержащие, и не содержащие К. Как правило, К содержит свободный член характеристического уравнения.
Поэтому запишем характеристическое уравнение в виде:
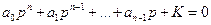 .
.
Подставим в него
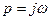
и разрешим это уравнение относительно К
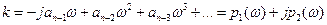
Изменяя 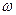 от
от 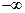 до
до 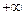 , построим границу области, претендующей на устойчивость.
, построим границу области, претендующей на устойчивость.
 Для того чтобы определить область , претендующую на устойчивость, воспользуемся правилом штриховки.
Для того чтобы определить область , претендующую на устойчивость, воспользуемся правилом штриховки.
Если мы передвигаемся по мнимой оси от 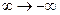 к
к 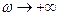 , то область устойчивости остается слева, поэтому, передвигаясь по выделенной границе от
, то область устойчивости остается слева, поэтому, передвигаясь по выделенной границе от 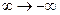 к ,
к , 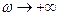 штрихуем левую сторону
штрихуем левую сторону
кривой. Полностью заштрихованная область есть область, претендующая на устойчивость.
Чтобы проверить, будет эта область областью устойчивости, возьмем любую точку из этой области, подставим в ее в характеристическое уравнение и проверим САУ на устойчивость. Если в данной точке система устойчива, значит выделенная область является областью устойчивости. Т.к. К – вещественная, положительная величина, то система устойчива от 0 до 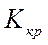
Пример.
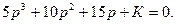
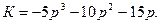
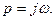
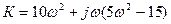 =
= 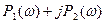
Строим годограф.
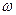
| Р1 | Р2 |
| -10 | ||
| -1 | ||
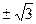
| ||
| -2 | -10 |
Строим годограф. Он пересекает вещественную ось при 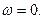
(Р1=0, Р2=0) и при 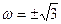 (Р1=30, Р2=0)
(Р1=30, Р2=0)

Проверяем выделенную область на устойчивость. Берем К=1.
Подставляем в характеристическое уравнение:
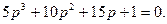
По критерию Гурвица 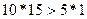 Следовательно, выделенная область является областью устойчивости.
Следовательно, выделенная область является областью устойчивости.
САУ устойчива при изменении К от 0 до 30.
D – разбиение в плоскости 2-х параметров.
Для того, чтобы можно было провести D – разбиение в плоскости 2-х параметров, нужно, чтобы эти параметры входили в характеристическое уравнение линейно-независимо.
Пусть параметры, в плоскости которых хотим выделить область устойчивости, будут 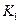 и
и 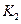 .
.
Выделим в характеристическом уравнении, члены содержащие 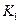 и
и 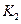 , и не содержащие ни того, ни другого.
, и не содержащие ни того, ни другого.
Тогда характеристическое уравнение запишется
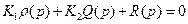 (1)
(1)
Т.к. границами устойчивости являются мнимая ось и уравнение корня, лежащего на ней 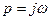 . Подставим значения этого корня в характеристическое уравнение.
. Подставим значения этого корня в характеристическое уравнение.
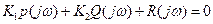 ( 2)
( 2)
Выделим в каждом члене уравнения (2) действительную и мнимую части.
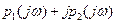
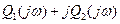
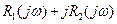 (3)
(3)
Тогда уравнение перепишется в виде
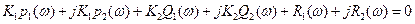 (4)
(4)
Уравнение (4) комплексное число. Оно равно нулю, если равны нулю вещественная и мнимая части
Вещественная: 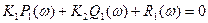 (5)
(5)
Мнимая: 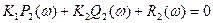
Получили два уравнения с двумя неизвестными. Решим их относительно 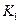 и
и 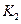 , воспользовавшись правилом Крамера.
, воспользовавшись правилом Крамера.
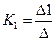
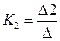 (6)
(6)
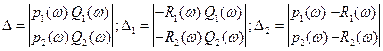
С помощью уравнения (6), мнимая ось отображается на плоскость параметров регулятора 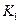 -
- 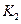 .
.
Если 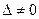 , то каждому значению
, то каждому значению 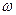 соответствуют определенные значения
соответствуют определенные значения 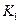 и
и 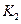 .
.
При непрерывном изменении 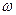 на плоскости
на плоскости 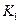 -
- 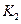 вычерчивается кривая, которая представляет собой границу области с одинаковым распределением корней.
вычерчивается кривая, которая представляет собой границу области с одинаковым распределением корней.
Проанализируем 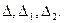
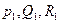 - четные функции частоты
- четные функции частоты
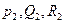 - нечетные функции частоты
- нечетные функции частоты
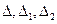 - нечетные функции частоты.
- нечетные функции частоты.
Следовательно, 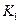 и
и 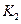 - четные функции частоты, т.е. полиномы, определяющие
- четные функции частоты, т.е. полиномы, определяющие 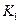 и
и 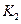 , содержат только четные функции от
, содержат только четные функции от 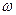 .Т.о значениям
.Т.о значениям 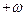 и
и 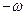 соответствует одна и та же точка кривой. Таким образом, при изменении
соответствует одна и та же точка кривой. Таким образом, при изменении 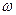 от
от 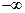 до
до 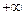 , кривая границы устойчивости пробегается дважды в противоположных направлениях и одна из сторон в выделенной области оказывается заштрихованной дважды.
, кривая границы устойчивости пробегается дважды в противоположных направлениях и одна из сторон в выделенной области оказывается заштрихованной дважды.
Область устойчивости в плоскости K1,-K2 при возрастании 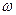 от 0 до
от 0 до 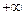 , при
, при 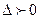 будет расположена слева, а при
будет расположена слева, а при 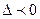 справа.
справа.
Т.к. 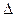 является непрерывной функцией частоты, то знак его может поменяться только при переходе
является непрерывной функцией частоты, то знак его может поменяться только при переходе 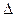 через 0. При этом момент прохождения
через 0. При этом момент прохождения 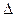 через 0, может соответствовать двум случаям:
через 0, может соответствовать двум случаям:
1) 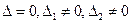 (в этом случае
(в этом случае 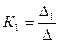 и
и 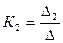 обращаются в
обращаются в 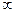 и переход
и переход 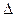 через 0 происходит в бесконечно удаленной точке границы устойчивости, а на всем протяжении границы
через 0 происходит в бесконечно удаленной точке границы устойчивости, а на всем протяжении границы 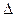 - знак не меняет)
- знак не меняет)
2) 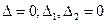 В этом случае, уравнения (5) являются одно следствием другого и отличаются они лишь постоянными множителями.
В этом случае, уравнения (5) являются одно следствием другого и отличаются они лишь постоянными множителями.
В этом случае при частоте 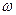 , где
, где 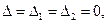 вместо одной точки, получаем бесконечную совокупность точек, лежащих на одной прямой. Эта прямая называется особой прямой . Она будет либо пересекать границу устойчивости, либо проходить через ее начало. В большинстве случаев особые прямые соответствуют
вместо одной точки, получаем бесконечную совокупность точек, лежащих на одной прямой. Эта прямая называется особой прямой . Она будет либо пересекать границу устойчивости, либо проходить через ее начало. В большинстве случаев особые прямые соответствуют 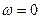 или
или 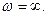
Особые прямые бывают в тех случаях, когда один из параметров К1 или К2 входит в свободный член характеристического уравнения.
Особые прямые штрихуются одинарными штрихами.
Выделенная область должна быть проверена на устойчивость по любому из критериев.
Пример.
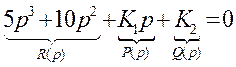
Подставим в это характеристическое уравнение корень, лежащий на мнимой оси, 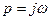
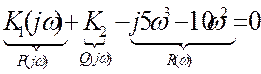
Разобьем на действительную и мнимую части
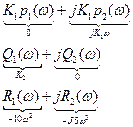
Таким образом, вещественная часть (только коэффициенты)
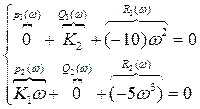
Получили систему

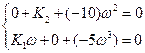
Таким образом 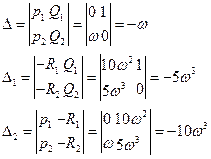
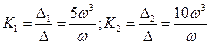
При 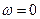 будет особая прямая.
будет особая прямая.
Построим эту границу
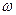
| |||
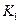
| |||
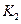
|


Особая прямая - 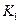 , при этом она штрихуется навстречу выделенной границы.
, при этом она штрихуется навстречу выделенной границы.
Проверим на устойчивость
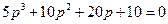
Гурвиц:
1) 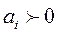
2) 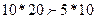
Т.к. в данной точке САУ устойчива, то выделенная область является областью устойчивости.
Иногда выделить область устойчивости в плоскости 2-х параметров можно даже, если они входят в характеристическое уравнение линейно независимо.
Пример.
Пусть характеристическое уравнение: 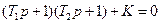
Хотим провести D – разбиение в плоскости 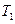 и
и 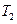
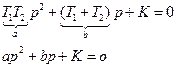
Проводим D – разбиение в плоскости а-в рассмотренным выше способом, т.к. они входят в уравнение линейно независимо.
Лекция 9
Качество систем автоматического управления.
Устойчивость является необходимым, но не единственным требованием, предъявляемым к системам управления. Устойчивость гарантирует сходимость переходного процесса к заданному значению регулируемой величины, а как быстро это происходит, насколько велики выбросы, какова точность, т.е. каково качество переходного процесса – эти вопросы остаются без ответа.
Однако к качеству переходного процесса часто предъявляет очень жесткие требования. Качество переходного процесса оценивается по реакции системы на типовые воздействия, такие как скачок, линейно возрастающее воздействие ( т.е. воздействие, возрастающее с постоянной скоростью), парабола ( т.е. воздействие, изменяющееся с постоянным ускорением).
Реакция системы на единичное скачкообразное воздействие называется переходной функцией и по ней чаще всего оценивают качество переходного процесса.
Качество оценивается по показателям качества.

Наиболее распространенными показателями качества являются:
1) динамическая ошибка – разность между 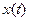 и
и 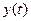
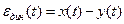 в данный момент времени
в данный момент времени
2) максимальное значение регулируемой величины 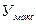
3) установившееся значение регулируемой величины 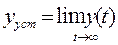
4) статическая ошибка 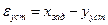
5) перерегулирование 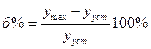 - превышение (выброс) над установившемся значением.
- превышение (выброс) над установившемся значением.
6) время переходного процесса 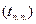 - время от момента подачи воздействия до момента, когда переходный процесс входит в зону заданной точности управления
- время от момента подачи воздействия до момента, когда переходный процесс входит в зону заданной точности управления 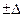 и больше из нее не выходит.
и больше из нее не выходит. 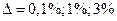 от
от 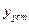 (обычно) Для того, чтобы оценить качество переходного процесса нужно построить переходный процесс.
(обычно) Для того, чтобы оценить качество переходного процесса нужно построить переходный процесс.
Методы построения переходного процесса.
(способы решения дифференциальных уравнений)
1. Непосредственное решение дифференциальных уравнений по корням характеристического уравнения.
2. Использование преобразований Фурье, Лапласа (Карсона-Хевисайда)
3. Использование вычислительных машин для решения дифференциальных уравнений. При этом используются аналоговые вычислительные машины (АВМ) и цифровые вычислительные машины (ЦВМ) При использовании АВМ строится электронный аналог математической модели САУ. Это означает, что на усилителях постоянного тока набираются типовые элементарные звенья, входящие в математическую модель САУ

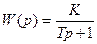
Из таких блоков состоит структурная схема САУ . Изменение напряжения на выходе системы будет аналогом изменения регулируемой величины. Решение дифференциальных уравнений на АВМ происходит непрерывно. Точность решения невысокая.
В ЦВМ при решении дифференциальных уравнений используются приближенные методы решения дифференциальных уравнений. Точность решения дифференциальных уравнений высокая.
Кроме оценки качества по переходным процессам применяются косвенные методы оценки качества:
1. По корням характеристического уравнения.
2. По частотным характеристикам.
3. Интегральные оценки качества.
Оценка качества по распределению корней характеристического уравнения.
Из курса математики известно, что решение неоднородного дифференциального уравнения
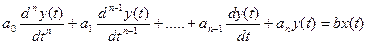 , (1)
, (1)
удовлетворяющего любым начальным условиям, в общем случае состоит из суммы двух слагаемых:
1) частного решения неоднородного уравнения, правая часть которого 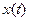 отлична от нуля и которое характеризует вынужденные колебания системы под действием возмущающих сил;
отлична от нуля и которое характеризует вынужденные колебания системы под действием возмущающих сил;
2) общего решения однородного уравнения
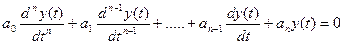 (2)
(2)
определяющего свободные (собственные) колебания системы после исчезновения возмущающих сил.
Уравнению (2) соответствует характеристическое уравнение:
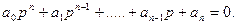 (3)
(3)
При исследовании устойчивости систем нас интересуют только свободные колебания, так как вся теория устойчивости основана на использовании понятия кратковременных возмущающих сил типа дельта функции 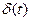 .
.
Общее решение однородного дифференциального уравнения, вызванное отклонением начальных условий от нулевых начальных условий, записывается
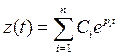
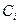 - постоянные интегрирования, определяемые начальными условиями
- постоянные интегрирования, определяемые начальными условиями
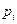 - корни характеристического уравнения (3)
- корни характеристического уравнения (3) 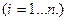
Отсюда видно, что характер переходного процесса зависит от расположения корней характеристического уравнения.
1) Пусть 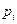 вещественные корни
вещественные корни 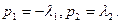

Если корни расположены на мнимой оси, то процесс никогда не затухает, так как 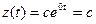 Чем ближе к мнимой оси расположен корень, тем дольше длится процесс. Таким образом, наибольший вес в общем решении имеют те составляющие решения, корни которых ближе расположены к мнимой оси. Если корень расположен в правой полуплоскости, то решение будет неограниченно возрастать.
Чем ближе к мнимой оси расположен корень, тем дольше длится процесс. Таким образом, наибольший вес в общем решении имеют те составляющие решения, корни которых ближе расположены к мнимой оси. Если корень расположен в правой полуплоскости, то решение будет неограниченно возрастать.
Степенью устойчивости 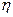 асимптотически устойчивой системы называется расстояние от мнимой оси до ближайшего корня.
асимптотически устойчивой системы называется расстояние от мнимой оси до ближайшего корня.
Зная 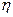 ,можно приближенно оценить время переходного процесса , считая, что когда общие решения от других, более далеких от мнимой оси корней затухнут, общее решение будет определяться корнем
,можно приближенно оценить время переходного процесса , считая, что когда общие решения от других, более далеких от мнимой оси корней затухнут, общее решение будет определяться корнем 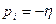 :
:
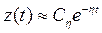
Можно показать, что
 Отсюда
Отсюда 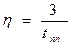
Действительно, если 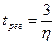 , то
, то 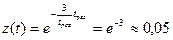
Т.о. за время 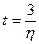 процесс уменьшится на 95%.
процесс уменьшится на 95%.
Можно по другому:
Положив в конце переходного процесса 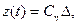 где
где 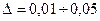 , полагая, что прошло 99-95% процентов переходного процесса, можем записать
, полагая, что прошло 99-95% процентов переходного процесса, можем записать
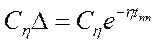 ,
, 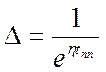 ,
, 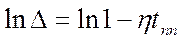 ,
, 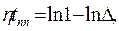
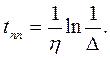
2) Корни комплексно сопряженные 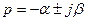
Вспомним формулу Эйлера 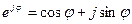
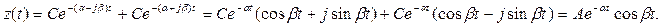
Если в системе комплексно- сопряженные корни, то будет колебательный переходный процесс.
 Если корни на мнимой оси, то колебательный процесс никогда не затухнет.
Если корни на мнимой оси, то колебательный процесс никогда не затухнет.
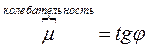 =
= 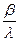
Если 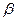 увеличивается , то колебательность возрастает.
увеличивается , то колебательность возрастает.
Чем больше 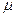 , тем больше колебания в системе.
, тем больше колебания в системе.
Если 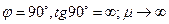 колебание никогда не затухнет
колебание никогда не затухнет
Если 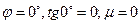 колебаний не будет, таким образом, по расположению корней характеристического уравнения можно оценить качество переходного процесса.
колебаний не будет, таким образом, по расположению корней характеристического уравнения можно оценить качество переходного процесса.
Диаграмма Вышнеградского
Оценка качества системы по корням характеристического уравнения третьего порядка.
Область устойчивости делится на 3 части.
Определяем рабочую точку, какое расположение корней, такой и будет переходный процесс. 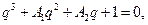 где
где 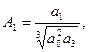
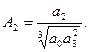
|

По заданным коэффициентам 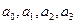 находим
находим 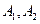
Определяем рабочую точку ( 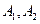 ). В какую область эта точка попала, такой переходный процесс и будет.
). В какую область эта точка попала, такой переходный процесс и будет.
Частотные критерии оценки качества.
Переходные функции и частотные характеристики связаны между собой через преобразование Фурье.

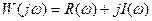
Обратное преобразование Фурье 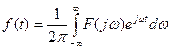
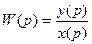 ,
, 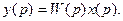 Если
Если 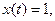 то
то 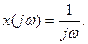 Тогда
Тогда 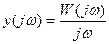 и
и 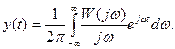
Таким образом, по поведению частотных характеристик можно судить о характере протекания переходной функции.
Наиболее удобной для оценки качества переходных процессов является амплитудно-частотная характеристика (АЧХ). Косвенным показателем качества переходного процесса является полоса пропускания АЧХ

Используя предельные соотношения преобразований Лапласа и Фурье, получим
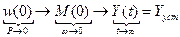
Т.е. установившееся значение выходной величины САУ равно значению АЧХ 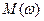 при
при 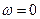 . Чем больше срезано низких частот, тем меньше установившееся значение выходной величины.
. Чем больше срезано низких частот, тем меньше установившееся значение выходной величины.
С другой стороны
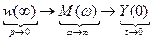
т.е. начало переходного процесса (поведение переходного процесса вблизи нуля) определяется высокочастотными составляющими спектра.
Чем больше в спектре высоких частот, тем круче, быстрее идет переходный процесс. Следовательно, чем шире полоса пропускания в АЧХ, тем быстрее будет идти переходный процесс.

Если в АЧХ появляется выброс, это говорит о том, что переходный процесс – колебательный, таким образом, по виду АЧХ можно оценивать качество переходных процессов.
Интегральные критерии оценки качества.
Здесь при оценке качества переходного процесса в качестве критерия оценки используют интеграл от переходного процесса.
Интегральные критерии оценки качества относятся к косвенным оценкам качества лишь исторически, т.к. раньше их считали по передаточным функциям по специальным формулам. Сейчас, при наличии персонального компьютера, интегральные оценки считаются по переходному процессу.
При монотонном переходном процессе в качестве интегральных оценок обычно используют линейные интегрированные оценки.

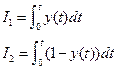
Такие интегральные оценки используются для монотонных и апериодических переходных процессов.
Чем больше 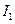 , тем лучше переходный процесс.
, тем лучше переходный процесс.
Чем меньше 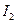 , тем лучше переходный процесс
, тем лучше переходный процесс
Для колебательных переходных процессов используют
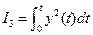 или
или 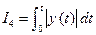

В случае необходимости в интегральной оценке можно учитывать и скорость протекания переходного процесса, добавляя в подынтегральное выражение производную от выходной величины.
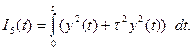
Минимум этой оценки соответствует приближению переходного процесса к экспоненциальному.
Интегральные оценки – относительные. Например, если 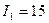 , нельзя оценить , хороший этот процесс или плохой. Если при других параметрах САУ мы получим
, нельзя оценить , хороший этот процесс или плохой. Если при других параметрах САУ мы получим 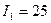 , то можно утверждать, что при этих параметрах переходный процесс лучше.
, то можно утверждать, что при этих параметрах переходный процесс лучше.
Лекция 10
Дата добавления: 2019-09-30; просмотров: 904;











