Критерии устойчивости САУ.
Это искусственные приемы, которые позволяют, не находя корней характерного уравнения, ответить на вопросы об устойчивости САУ, т.е. определять знаки вещественных частей корней.
Два вида критериев устойчивости:
1). Алгебраический критерий устойчивости (критерий устойчивости Гурвица).
Пусть заданно характерное уравнение .
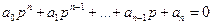
Для устойчивости САУ необходимо и достаточно:
1). Чтобы все коэффициенты характеристического уравнения имели бы один знак - 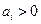 (
(  система не устойчива)
система не устойчива)
2). Главный определитель Гурвица, составленный по определенному правилу, и все его диагонали миноры имели бы знак коэффициентов - были бы больше нуля.
Правила написания главного определения Гурвица.
1). По главной диагонали определителя располагаются все коэффициенты характеристического уравнения в порядке возрастания индексов, начиная с a1.
2). Места в определителе над главной диагональю заполняются коэффициентами характеристического уравнения в порядке возрастания индексов.
3). Места в определителе под главной диагональю заполняются коэффициентами характерного уравнения в порядке убывания индексов.
4). Места в определителе, где должны стоять коэффициенты с индексами больше n и меньше нуля, заполняются нулями
Таким образом главный определитель Гурвица имеет вид:
 A=
A= 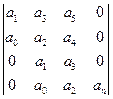 >0
>0 
САУ устойчива, если
1). Все коэффициенты характеристического уравнения больше нуля ( 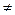 0!)
0!)
 ,
, 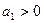 , ….
, …. 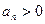
2). Главный определитель Гурвица и все его диагональные миноры > 0.
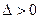 ,
, 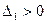 ,
, 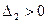 , ….
, …. 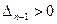
Рассмотрим примеры.
1. 
1. 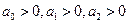
2. 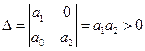
Для устойчивости САУ второго порядка необходимым и достаточным условием устойчивости является положительность коэффициентов характеристического уравнения.
2. 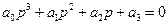
1. 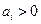 i=0…3
i=0…3
2. 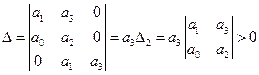

Необходимым и достаточным условием устойчивости систем третьего порядка является положительность коэффициентов и произведение внутренних членов 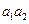 должно быть больше произведения крайних членов
должно быть больше произведения крайних членов 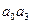 характеристического уравнения.
характеристического уравнения.
3. 
 ,
, 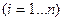
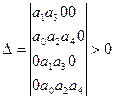
 ,
, 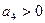 ,
, 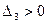
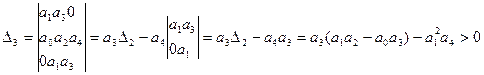
Есть еще алгебраический критерий Рауса. Это тот же критерий Гурвица, но организованный таким образом, что по нему удобно составлять программы для определения устойчивости.
Критерий устойчивости Вышнеградского для систем третьего порядка.
Вышнеградский И.А. предложил изображать границу устойчивости на так называемой плоскости параметров Вышнеградского.
Пусть имеем характеристическое уравнение третьей степени.
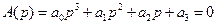
Преобразуем его с помощью подстановки:
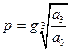
Тогда оно примет вид:


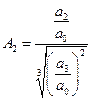
A1 и A2 называются параметрами Вышнеградского (безразмерные величины), в плоскости которых строится граница устойчивости.
Применим к преобразованному уравнению критерий устойчивости Гурвица
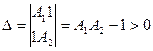
или A1 A2 > 1
На границе устойчивости 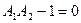 .
.
Отсюда 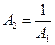 - уравнение на границе устойчивости
- уравнение на границе устойчивости


По коэффициентам характеристического уравнения определяются А1 и А2 . Если точка оказалась ниже гиперболы – САУ устойчива, выше - неустойчива.
Дата добавления: 2019-09-30; просмотров: 731;











