ВЗАМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ

Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную другой плоскости.

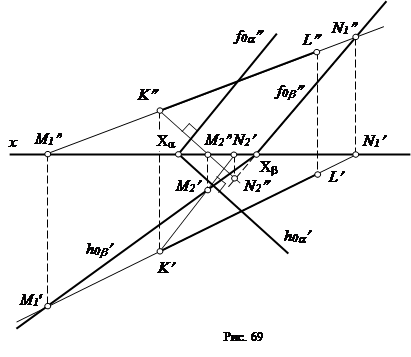
На рис. 69 дано построение плоскости b, перпендикулярной плоскости a и проходящей через прямую KL. Из любой точки прямой KL, например, из точки К, проводим перпендикуляр к заданной плоскости a. Строим следы прямой KL и перпендикуляра: проекции горизонтального и фронтального следов прямой KL (M₁¢ и M₁², N₁¢ и N₁¢¢) и перпендикуляра (M₂¢ и M₂², N₂¢ и N₂¢¢) .

Через горизонтальные проекции горизонтальных следов M₁¢и M₂¢ проводим горизонтальный след плоскости b; через фронтальные проекции фронтальных следов N₁² и N₂² - фронтальный след b. Проверяем правильность построений: следы h_0b¢ и f_0b² должны пересечься в точке схода следов Х_b на оси x.

Таким образом, плоскость b перпендикулярна плоскости a (однако их одноименные следы в общем случае не перпендикулярны друг другу).

Лекция 6

ОСНОВЫ ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ.

СУЩНОСТЬ МЕТОДА.

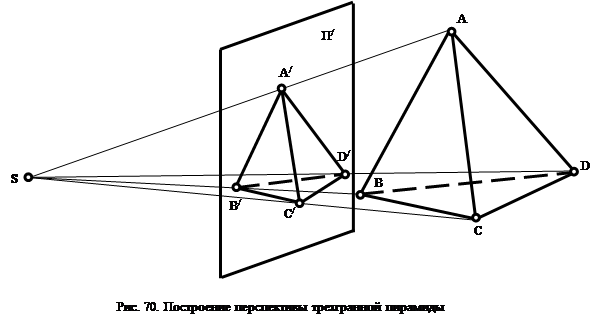Перспектива представляет собой способ изображения тел и плоских фигур, основанный на применении центрального проецирования. Для построения перспективы предмета из некоторой точкиS (точки зрения)проводят лучи ко всем точкам изображаемого предмета. На пути проецирующих лучей располагают поверхность П^’ (картину), на которой строят искомое изображение, определяя точки пересечения лучей с поверхностью картины (рис.70).

Метод отличается хорошей наглядностью, перспектива предмета соответствует тому, что видит глаз человека (передает кажущиеся изменения формы и размеры предмета, вызванные его расположением и удаленностью от наблюдателя), поэтому этот метод нашел широкое распространение в архитектурном проектировании, в строительном деле, геодезии и других прикладных науках.

В зависимости от поверхности, на которую производится проецирование, следует различать перспективу плоскую (П^/ - плоскость), панорамную (П^/ - цилиндрическая поверхность) и купольную (П^/ - сфера).

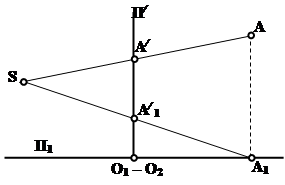
Для того, чтобы обеспечить взаимную однозначность между точками изображаемого предмета и точками на картинной плоскости (сделать изображение обратимым), заданную точку А ортогонально проецируют на горизонтальную плоскость П₁, а затем на плоскости картины П^/ определяют перспективные проекции А^/ и А₁^/ соответственно точки А и ее горизонтальной проекции А₁. Проекция А^/ точки А называется перспективной проекцией (перспективой) точки А, а проекция А₁^/ - вторичной проекцией точки А. На плоскости П^/ проекции А^/ и А₁^/ принадлежат одной вертикальной прямой, так как лежат в лучевой плоскости, перпендикулярной плоскости П₁.

Из рис. 71 и 72 видно, что по заданным проекциям А^/ и А₁^/ и точке S можно однозначно определить положение точки А в пространстве.

	Рис. 72. Построение перспективы и вторичной проекции точки