Взаимная принадлежность точки, прямой и плоскости

Комплексный чертёж плоскости и поверхности

В данном модуле вы познакомитесь с различными видами поверхностей и их модификациями, способами задания их на комплексном чертеже, особенностями построения. Узнаете, что простейшая поверхность - это плоскость.

Задание плоскости на комплексном чертеже

«Поверхность есть то, что имеет только длину и ширину»

(Евклид «Начала», 4 век до н.э., книга 1, определение 5.)

Как вы думаете?

1. Не дана ли в "Началах" трактовка поверхности слишком упрощенно?
2. Какая фигура в современном понимании имеет "только длину и ширину"?
3. Безразмерна ли плоскость, или она имеет границы?
4. Можно ли задать плоскость пространственными линиями?

Плоскость является частным случаем поверхности - это двумерная геометрическая фигура, она имеет только длину и ширину, и не имеет толщины. Обозначается прописными буквами греческого алфавита. Плоскость - это множество точек, но определяется она тремя точками (напомним, что прямую линию определяют две точки).

Плоскость можно задать на чертеже:

1. Тремя точками: S(А, В, С);

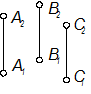
1. Прямой и точкой, не лежащей на данной прямой: Г(а, В);

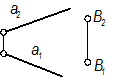
Двумя параллельными прямыми: D(с|| а);

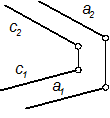
1. Двумя пересекающимися прямыми: F(m Ç n);

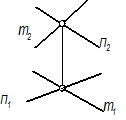
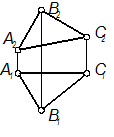
1. Любой плоской фигурой: L(АВС);

1. Своей главной проекцией: W(W­₁);

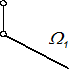
1. Линией наибольшего наклона плоскости Q (g₁ ,g₂);

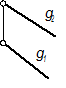
Рис. 2-1

Плоскости бывают общего и частного положения

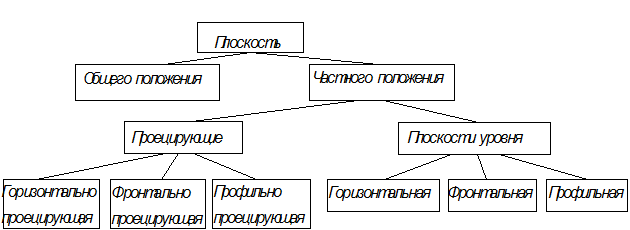
Рис. 2-2

Если плоскость не перпендикулярна ни одной из плоскостей проекций,

то она называется плоскостью общего положения

Примеры чертежа плоскости общего положения см. варианты 1 - 5; 7 (рис. 2-1).

Взаимная принадлежность точки, прямой и плоскости