ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ
В каждой плоскости можно провести бесчисленное множество прямых линий частного положения.
Горизонталь плоскости– это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций p1. Она обладает всеми свойствами горизонтальной прямой: ее фронтальная проекция параллельна оси x, а на горизонтальную плоскость проекций она проецируется в истинную величину (рис. 39).
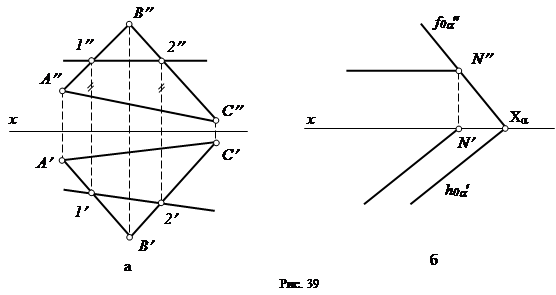 |
Если плоскость задана следами (рис. 39, б), то горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.
Фронталь плоскости –это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций. Горизонтальная проекция фронтали параллельна оси x, а фронтальная проекция – есть ее истинная величина (рис. 40).
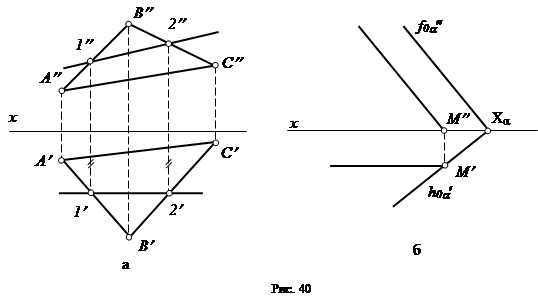 |
Фронтальная проекция фронтали параллельна фронтальному следу плоскости, в которой лежит данная фронталь. (рис. 40, б).
ЛИНИЯ НАИБОЛЬШЕГО СКАТА ПЛОСКОСТИ
Линия наибольшего ската – это прямая, лежащая в плоскости и перпендикулярная следу или линиям частного положения плоскости (в нашем примере на рис. 41 – перпендикулярная горизонталям этой плоскости).
Из всех прямых, принадлежащих плоскости, линия наибольшего ската имеет самый большой угол наклона к соответствующей плоскости проекций (в нашем примере на рис. 41 – к горизонтальной плоскости проекций p1), который называется
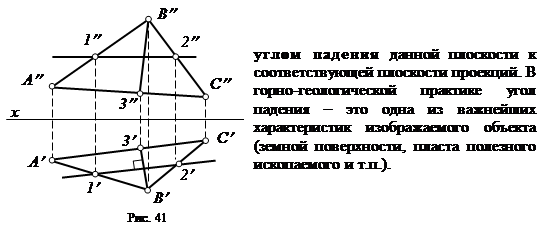 |
ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ПЛОСКОСТИ
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.
Рассмотрим пример: через точку К провести прямую, параллельную плоскости a, заданной следами (рис. 42).
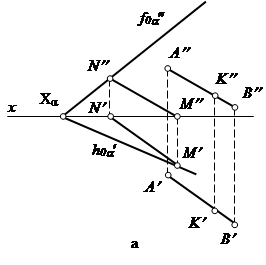
 Проведем в плоскости a любую прямую, например, прямую MN (рис. 42, а). Затем через точку К параллельно MN проведем прямую АВ. Эта прямая будет параллельна плоскости a, так как она параллельна прямой MN, лежащей в этой плоскости.
Проведем в плоскости a любую прямую, например, прямую MN (рис. 42, а). Затем через точку К параллельно MN проведем прямую АВ. Эта прямая будет параллельна плоскости a, так как она параллельна прямой MN, лежащей в этой плоскости.
|
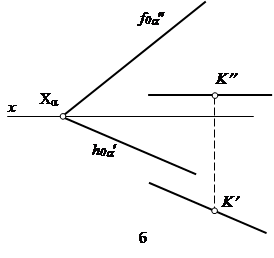
Эту же задачу, можно решить другим способом, проведя через точку К прямую частного положения, например, горизонтальную прямую (рис. 42, б). Горизонтальная проекция горизонтальной прямой проходит через проекцию К¢ и параллельна следу h0a¢.
Если плоскость задана не следами, а иным способом (двумя пересекающимися прямыми, двумя параллельными прямыми, плоской фигурой и т.д.), то через заданную точку также можно провести прямую, параллельную любой прямой, лежащей в заданной плоскости. В качестве такой прямой может быть выбрана одна из прямых,
которыми задана сама плоскость.

ТОЧКА В ПЛОСКОСТИ
Точка лежит в плоскости, если она лежит на прямой, принадлежащей этой плоскости.
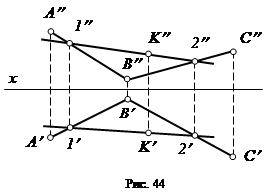 Пример 5. Построить недостающую проекцию точки К, лежащей в заданной плоскости (плоскость задана двумя пересекающимися прямыми АВ и ВС, а точка – только ее фронтальной проекцией К¢¢, рис. 44).
Пример 5. Построить недостающую проекцию точки К, лежащей в заданной плоскости (плоскость задана двумя пересекающимися прямыми АВ и ВС, а точка – только ее фронтальной проекцией К¢¢, рис. 44).
1. Через точку К проведем произвольную прямую 1-2, принадлежащую заданной плоскости:
К¢¢ Î 1¢¢2¢¢.
2. Построим горизонтальные проекции точек 1¢ и 2¢.
3. Через 1¢ и 2¢ проводим горизонтальную проекцию прямой 1-2.
4. В пересечении линии проекционной связи, проведенной из К¢¢ и 1¢-2¢ находим горизонтальную проекцию точки К.
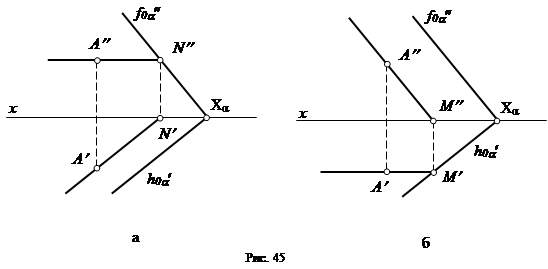 Если плоскость задана следами, то недостающая проекция точки, принадлежащей заданной плоскости, может быть найдена при помощи горизонтали (рис. 45, а) или фронтали (рис. 45, б) плоскости.
Если плоскость задана следами, то недостающая проекция точки, принадлежащей заданной плоскости, может быть найдена при помощи горизонтали (рис. 45, а) или фронтали (рис. 45, б) плоскости.
Лекция 5
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Две плоскости могут быть:
1) параллельными;
2) пересекающимися.
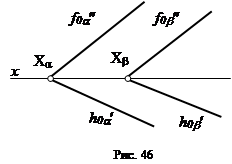
Если два следа одной плоскости параллельны одноименным следам другой плоскости, то такие плоскости взаимно параллельны (рис. 46).
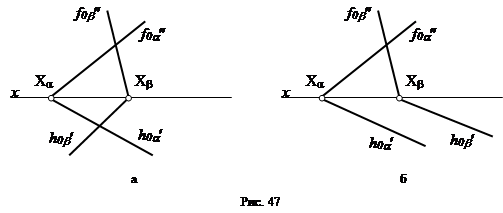
Если, хотя бы одна пара одноименных следов двух плоскостей пересекается, то эти плоскости пересекаются (рис. 47).
 |
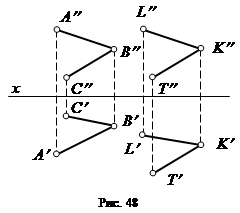
Когда плоскости заданы не следами, а иным способом, то две плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, например (рис. 48): АВ || КL и ВС || КТ.
ПЕРЕСЕКАЮЩИЕСЯ ПЛОСКОСТИ
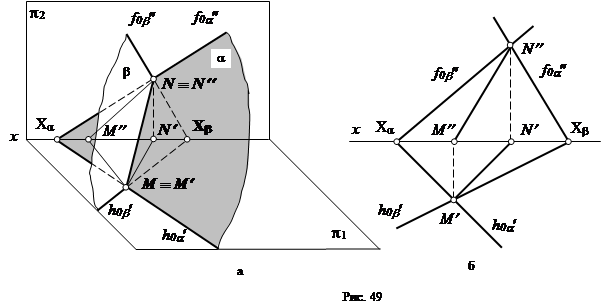
Линией пересечения двух плоскостей является прямая, все точки которой являются общими для обеих плоскостей. Таким образом, в общем случае для нахождения линии пересечения необходимо найти хотя бы две точки, общих для обеих плоскостей. Такими точками могут быть, например, точки пересечения одноименных следов плоскостей a и b – точки M и N (рис. 49, а). Через них и пройдет линия пересечения. Линия пересечения плоскостей видима только в 1-м октанте(значения координат х,у и z положительные).
На эпюре (рис. 49, б) проекции линии пересечения пройдут через точки пересечения одноименных следов плоскостей a и b. В пересечении горизонтальных следов находим проекцию общей точки М¢ (фронтальная проекция этой точки М¢¢ лежит на оси x), а в пересечении фронтальных следов - N¢¢ (горизонтальная проекция N¢ также лежит на оси x). Соединив одноименные проекции М и N, получим две проекции линии пересечения на эпюре.
Но далеко не всегда на эпюре мы можем найти эти точки. Рассмотрим несколько типовых примеров построения линии пересечения плоскостей.
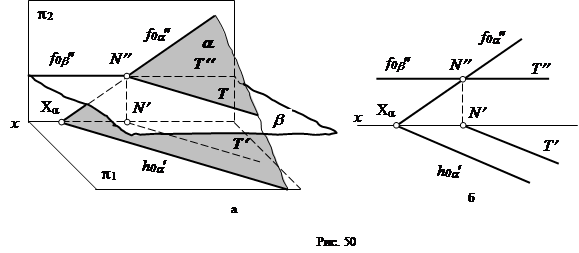
1) Пусть дана пара плоскостей, из которых одна – плоскость общего положения a (h0a¢, f0a²), а другая – горизонтальная плоскость b (f0b²) (рис. 50). Одна общая точка – точка N (N¢, N¢¢) - находится легко в пересечении фронтальных следов.
Но поскольку плоскость b - горизонтальная, она параллельна плоскости проекций p1, с ней не пересекается и не имеет горизонтального следа. Из школьного курса геометрии известно, что две параллельные плоскости пересекаются третьей плоскостью по параллельным прямым. Следовательно, линией пересечения плоскостей a и b будет горизонталь Т (Т¢, Т¢¢).
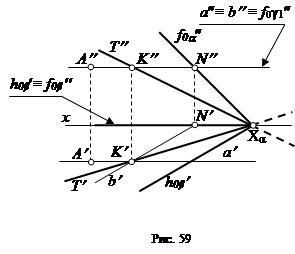
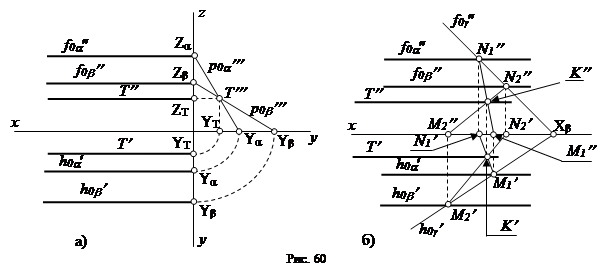
2) Соответственно линией пересечения плоскости общего положения α (h0α¢, f0α²) с фронтальной плоскостью γ (h0γ¢)будет фронталь плоскости T ( T¢, T¢¢) (рис. 51, а), а с профильной плоскостью β (h0b¢, f0b²) – профильная прямая плоскости T ( T¢, T¢¢, T¢¢¢) (рис. 51, б).

3) Теперь возьмем две плоскости общего положения a и b, у которых одноименные следы, например, фронтальные, в пределах чертежа не пересекаются (рис.52).
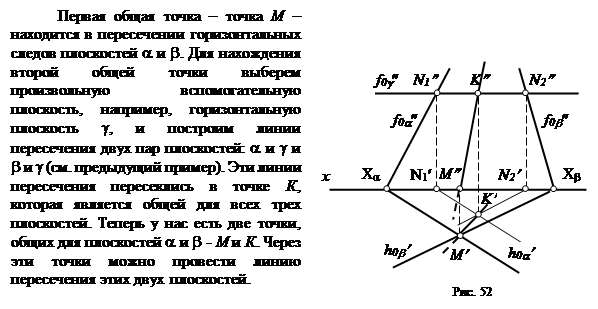 |
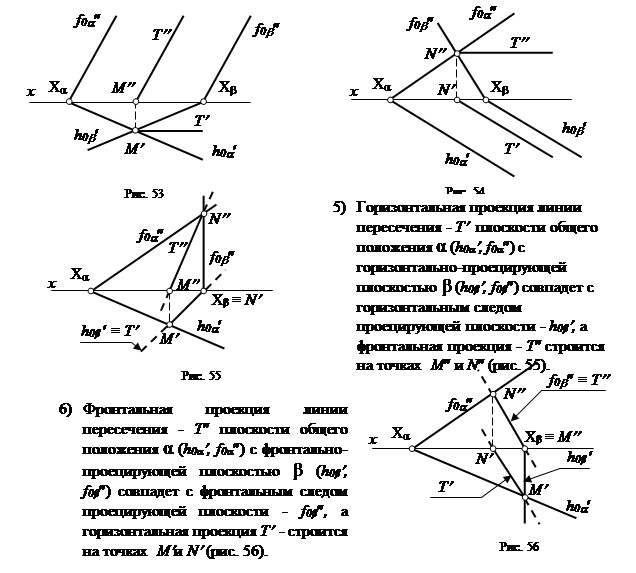
4) Если фронтальныеследы двух плоскостей параллельны, то линией их пересечения будет фронтальТ (Т¢,Т¢¢) (рис. 53). В этом легко убедиться, если воспользоваться вспомогательной горизонтальной плоскостью, как в предыдущем примере.
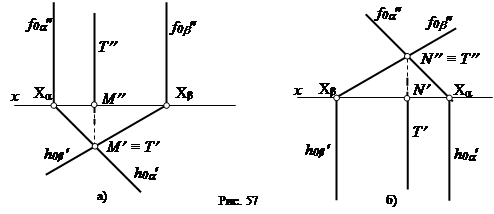
По аналогии можно сказать, что если у пересекающихся плоскостей параллельны горизонтальные следы, то линией их пересечения будет горизонтальТ (Т¢,Т¢¢) (рис.54).
 7) Еще более просто строится линия пересечения проецирующих плоскостей (рис. 57). Линия пересечения Т горизонтально-проецирующихплоскостей α (h0α¢, f0α²) и β (h0β¢, f0β²) представляет собой горизонтально-проецирующую прямую, фронтальная проекция Т² которой параллельна фронтальным следам плоскостей и проходит через проекцию М², а горизонтальная проекция Т¢ проецируется в точку, которая совпадает с проекцией пересечения горизонтальных следов плоскостей - М¢ (рис. 57,а).
7) Еще более просто строится линия пересечения проецирующих плоскостей (рис. 57). Линия пересечения Т горизонтально-проецирующихплоскостей α (h0α¢, f0α²) и β (h0β¢, f0β²) представляет собой горизонтально-проецирующую прямую, фронтальная проекция Т² которой параллельна фронтальным следам плоскостей и проходит через проекцию М², а горизонтальная проекция Т¢ проецируется в точку, которая совпадает с проекцией пересечения горизонтальных следов плоскостей - М¢ (рис. 57,а).
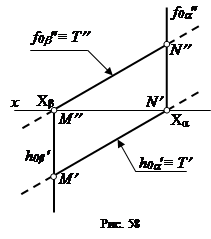
8) Линия пересечения Т фронтально-проецирующихплоскостей α (h0α¢, f0α²) и β (h0β¢, f0β²) представляет собой фронтально-проецирующую прямую, горизонтальная проекция Т¢ которой параллельна горизонтальным следам плоскостей и проходит через проекцию N¢, а фронтальная проекция Т² проецируется в точку, которая совпадает с проекцией пересечения фронтальных следов плоскостей - N²(рис. 57, б).
 |
|
|
|
ПРЯМАЯ, ПЕРЕСЕКАЮЩАЯ ПЛОСКОСТЬ
 Прямая, пересекающая плоскость, имеет с ней одну общую точку, называемую точкой встречи прямой с плоскостью.
Прямая, пересекающая плоскость, имеет с ней одну общую точку, называемую точкой встречи прямой с плоскостью.
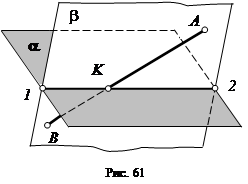
 Рассмотрим задачу о нахождении точки встречи прямой линии с плоскостью в общем виде (рис. 61). Пусть нам дана плоскость a и прямая АВ, ее пересекающая. Проведем через прямую АВ любую плоскость, например, плоскость b. Далее построим линию пересечения плоскости a и b - прямую 1-2. Все точки этой прямой являются общими для обеих плоскостей. Следовательно, и точка К, лежащая на прямой АВ, принадлежит обеим плоскостям. Точка К и будет искомой точкой встречи прямой АВ с плоскостью a.
Рассмотрим задачу о нахождении точки встречи прямой линии с плоскостью в общем виде (рис. 61). Пусть нам дана плоскость a и прямая АВ, ее пересекающая. Проведем через прямую АВ любую плоскость, например, плоскость b. Далее построим линию пересечения плоскости a и b - прямую 1-2. Все точки этой прямой являются общими для обеих плоскостей. Следовательно, и точка К, лежащая на прямой АВ, принадлежит обеим плоскостям. Точка К и будет искомой точкой встречи прямой АВ с плоскостью a.
Рассмотрим порядок действий по нахождению точки встречи прямой АВ с плоскостью a на эпюре (рис. 62):
1) Через заданную прямую АВ проводим любую вспомогательную плоскость (удобнее, если это будет плоскость частного положения – например, фронтально-проецирующая плоскость b).
2) Находим линию пересечения плоскостей a и b - прямую MN.
3) Горизонтальная проекция К¢ искомой точки встречи лежит в пересечении горизонтальных проекций прямой А¢В¢ и линии пересечения M¢N¢.
4) В пересечении линии проекционной связи, проведенной из К¢, и фронтальной проекции прямой получаем К¢¢.
ОПРЕДЕЛЕНИЕ ВЗАИМНОЙ ВИДИМОСТИ
ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ
Взаимная видимость геометрических элементов определяет позиционное отношение одной геометрической фигуры (прямой, плоскости и т.д.) по отношению к другой в определенном направлении. Обычно это направление перпендикулярно плоскости проекций.
Взаимная видимость на эпюре определяется с помощью конкурирующих точек1, которые выбираются на той плоскости проекций, в направлении на которую определяется взаимная видимость. Конкурирующими точкаминазываются точки, принадлежащие двум разным элементам проекции которых в одной плоскости проекций сливаются, а в другой плоскости проекций – расходятся по линии проекционной связи. Взаимная видимость в направлении на каждую из плоскостей проекций определяется отдельно.
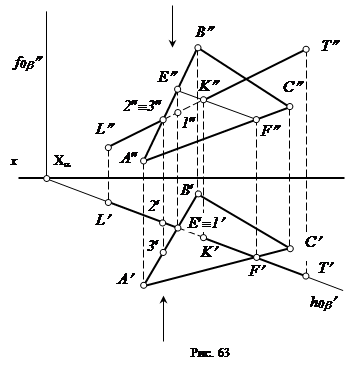 Рассмотрим определение взаимной видимости прямой LТ и плоскости, заданной треугольником АВС (рис. 63). Будем считать плоскость треугольника непрозрачной. Прежде всего найдем точку пересечения прямой LТ с плоскостью треугольника. Через прямую LТ проведем вспомогательную плоскость a и построим линию пересечения плоскости a и плоскости треугольника АВС – прямую EF . Найдем искомую точку К. Затем определяем взаимную видимость в направлении на плоскости проекций p1 и p2.
Рассмотрим определение взаимной видимости прямой LТ и плоскости, заданной треугольником АВС (рис. 63). Будем считать плоскость треугольника непрозрачной. Прежде всего найдем точку пересечения прямой LТ с плоскостью треугольника. Через прямую LТ проведем вспомогательную плоскость a и построим линию пересечения плоскости a и плоскости треугольника АВС – прямую EF . Найдем искомую точку К. Затем определяем взаимную видимость в направлении на плоскости проекций p1 и p2.
Для определения видимости в направлении на плоскость p1 выбираем конкурирующие точки, например, Е и 1 (E¢º1¢). Эти точки принадлежат разным геометрическим фигурам (Е Î АВ; 1 Î LТ), но они расположены на одной проецирующей прямой, перпендикулярной плоскости p1, поэтому на эту плоскость они проецируются в одну точку. Находим фронтальную проекцию точки 1 - 1¢¢ (проекция Е¢¢ уже была найдена при предыдущих построениях).
Из двух точек видимой будет та, фронтальная проекция которой расположена дальше от оси координат. В нашем примере – это точка Е. Следовательно, на горизонтальной проекции видимой будет прямая АВ, принадлежащая плоскости треугольника, а прямая LК – “невидима”. В точке К прямая LТ пересекает плоскость и отрезок КT cтанет видимым.
Для определения взаимной видимости в направлении на p2 выбираем на ней проекции конкурирующих точек. Пусть это будут точки 2² и 3¢¢ (2²º3²). Находим их горизонтальные проекции и определяем по ним взаимную видимость точек. Дальше от оси x будет точка 3¢, принадлежащая D АВС. Следовательно отрезок L¢¢К¢¢ - «невидим».
ПРОЕЦИРОВАНИЕ ПЛОСКИХ ФИГУР
Плоской фигурой называется такая фигура, все точки которой лежат в одной плоскости и ограничены линиями, составляющими контур этой фигуры. Простейшей плоской фигурой является многоугольник.
 Для определения однозначного положения в пространстве многоугольника необходимо убедиться, чтобы все точки этой фигуры находились в одной плоскости.
Для определения однозначного положения в пространстве многоугольника необходимо убедиться, чтобы все точки этой фигуры находились в одной плоскости.
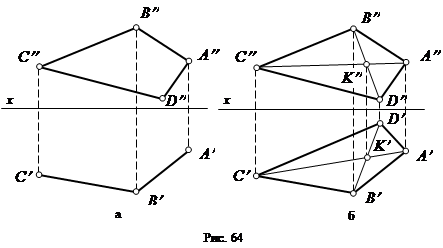
 Например, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис. 64). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многогранника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей K (K¢, K²).
Например, четырехугольник может быть задан двумя проекциями трех его вершин и лишь одной проекцией четвертой вершины (рис. 64). Недостающая проекция вершины лежит на пересечении линии проекционной связи, проведенной из имеющейся проекции вершины многогранника, и проекции диагонали, проходящей, в свою очередь, через точку пересечения диагоналей K (K¢, K²).
|
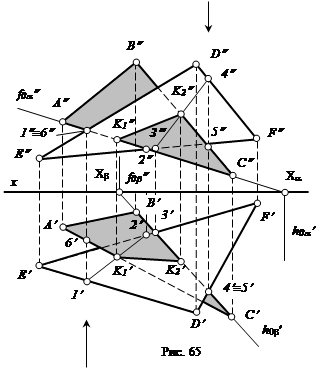
Аналогично находим точку K2 (K2¢, K2²) пересечения другой стороны, например, ВC треугольника EDF:
K2 = ВC Ç (∆ EDF).
Зная две точки, общие для заданных плоскостей (∆ АВС) и (∆ EDF), проводим через них линию пересечения этих плоскостей K1K2 (K1¢K2¢ и K1²K2²).
Определяем видимость плоскостей друг относительно друга с помощью конкурирующих точек, например, точек 4 и 5 – на горизонтальной плоскости проекций (4 Î (DF), 5 Î (BC)) и точек 1 и 6 – на фронтальной плоскости проекций (1 Î (ED),
6 Î (AC).
ПРЯМАЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ
Предположим, что дана некоторая плоскость a и прямая АК – перпендикуляр к этой плоскости, причем точка К является основанием перпендикуляра (рис. 66).
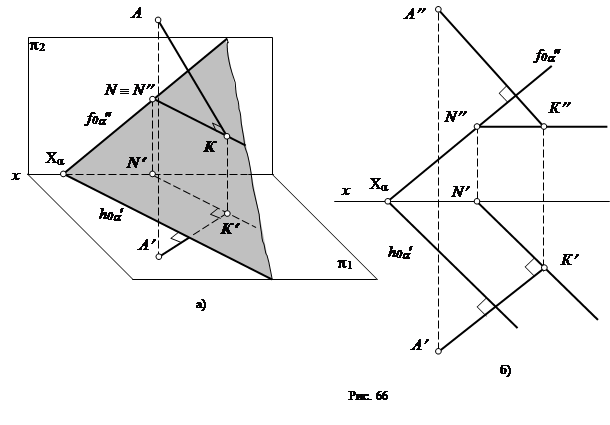
Если прямая АК – перпендикуляр, то она перпендикулярна любой прямой, принадлежащей этой плоскости.
Через точку К проведем горизонталь КN. Угол АКN – прямой. По теореме о том, что прямой угол проецируется на плоскость проекций без искажения, если хотя бы одна его сторона параллельна плоскости проекций, угол А¢К¢N¢ - тоже прямой.
Таким образом, горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали и горизонтальному следу плоскости.
Аналогично можно доказать, что фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали и фронтальному следу плоскости.
Пример 6. Из точки К опустить перпендикуляр к плоскости, заданной следами (рис. 67), и к плоскости, заданной треугольником (рис. 68).
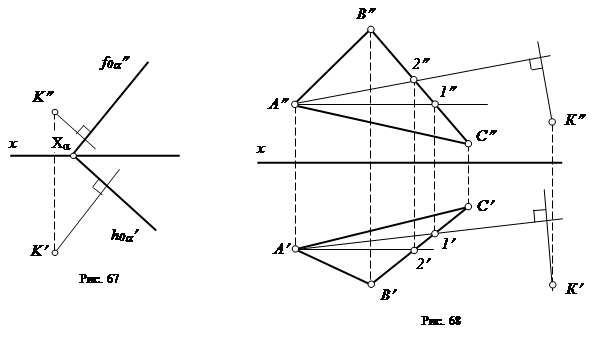 |
1. Из точки K проводим перпендикуляр к плоскости a, заданной следами, (рис. 67): горизонтальная проекция перпендикуляра перпендикулярна горизонтальному следу плоскости h0a¢; фронтальная проекция перпендикуляра перпендикулярна фронтальному следу плоскости f0a².
2. Из точки K проводим перпендикуляр к плоскости, заданной треугольником АВС, (рис. 68).
Строим горизонталь А1 (А²1², А¢1¢) и фронталь А2 (А¢2¢, А²2²) заданной плоскости.
Из точки К, проводим перпендикуляр к заданной плоскости: горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали А¢1¢; фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали А²2².
Дата добавления: 2017-01-08; просмотров: 5732;











