Парадокс Гиббса. К вопросу об аддитивности энтропии.

Формула (1) написана для 1 моля вещества, если же рассматриваем не 1 моль, тогда она примет следующий вид:

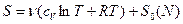
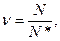где N* - число Авогадро.

Теперь пусть имеется сосуд, разделённый перегородкой на две равные части объёмом V каждая, N₁=N₂=N.

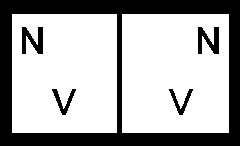
Если убрать перегородку, физическое состояние системы остаётся неизменным (тот же газ, те же параметры), естественно ожидать, что энтропия останется неизменной. Проверим:

1) до слияния

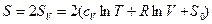(2)

2) после слияния

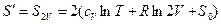. (3)

Учтём что c_V ~ N, R ~ N, (S₀ – также ~ N, т.к. выражение (*) можем поделить на N). Тогда (3)-(2):

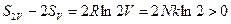(4)

Получили возрастание энтропии. Но система то одна! Парадокс Гиббса.

В чём дело? Гиббс предложил следующее:

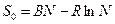(5)

где S₀не зависит от Т и V = const.

Тогда 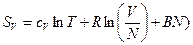и 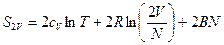и S_2V = 2S_V, парадокса нет, энтропия аддитивна. Но почему? Посмотрим на выражение для энтропии, которое из статистики. Была формула для F (F=U-TS) :

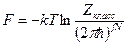и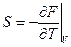

Было: .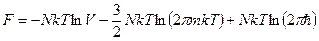

Отсюда:

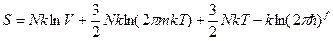(6)

(легко видать)

Сравним (6) и (1), (6) и (5) – отсутствует слагаемое с lnV. Почему? Т.е. или термодинамика, или классическая статистика не дают полного описания. Приходится опять возвращаться к вопросам нормировки функции распределения, что мы уже делали. Итак, если газ один, то нужно воспользоваться принципом тождественности частиц: если переставить 2 (поменять местами) частицы местами, то микросостояние системы не изменится (это не выполняется для различных газов),т.е. число микросостояний меньше, чем при прямом интегрировании.

Было: 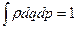, потом 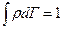, где 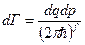- число микросостояний. А теперь учтём тождественность и поделим дополнительно на число перестановок (их N! штук):

Итак: 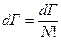(7), и это надо сделать для всего.

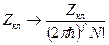(было без N!).

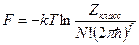(8)

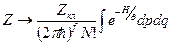. Учтём, что при N >> 1 справедлива формула Стирлинга (логарифм Стирлинга): 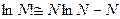. Тогда из (8) для S имеем:

,
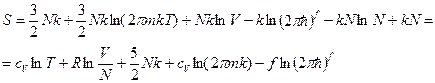где f ~ N. В результате S ~ N, аддитивная. 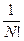можно не учитывать, если число частиц в системе постоянно. В противном же случае следует учитывать этот множитель.