Неравенство Клаузиуса. Превращение тепла в работу.

Вспомним II-ое начало термодинамики:

đQ*=TdS (1)

S – энтропия, функция состояния. Выражение (1) мы ввели для квазистатических процессов: 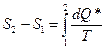, и для замкнутого квазистатического (обратимого) процесса выполнятся следующее:

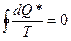(2)

- это равенство Клаузиуса. Что тогда получится для неравновесных процессов? Знаем, что энтропия растёт с течением времени (не убывает по крайней мере). Покажем это на основании I-го и II-го начал термодинамики.

Пусть есть некоорый переход 1→2 (неравновесный, необратимый). И есть (1→2) – обратимый и равновесный.

Тогда по I –му началу термодинамики:

đQ*_НП = dU + đA_НП (3)

и

đQ* = dU + đA

(U – функция состояния).

По равновесному обратимому процессу можем пройти обратно. Тогда рассмотрим круговой процесс: (1)→неравн→(2)→равнов→(1). Делаем (3)-(4), имеем (dU=dU=0),

đQ*_НП - đQ*= đA_НП – đA. (5)

1) Разность эта не может быть равна нулю, т.к. в этом случае можно было бы обратить равновесно неравновесный процесс без изменения в окружающих телах. (отдав тепло, đQ*_НП = đQ* и произведя работу đA_НП = đA).

2) Разность (5) не может быть больше нуля, т.к. в таком случае системой была бы произведена работа (đA_НП – đA>0) только за счёт теплоты теплоисточника без компенсации. Это противоречит II-му началу термодинамики. (вечный двигатель второго рода);

3) Разность (5) может быть меньше нуля. Это соответствует тому, что при возвращении системы в начальное состояние часть теплоты (đQ* - đQ*_НП). передаётся теплоисточнику за счёт внешней работы (đA - đA_НП) – это возможно. Осюда следует, что

đQ* > đQ*_НП (6)

đA > đA_НП (7)

Но т.к. đQ=TdS (равновесный процесс), то TdS > đQ_НП и

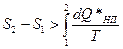(8)

Отсюда: при адиабатическом неравновесном процессе (đQ_НП = 0) энтропия растёт, dS>0, и S₂-S₁>0, т.е. пришли к тому же.

Иногда это условие: возрастание энтропии при неравновесных адиабатических процессах называется также вторым началом термодинамики для неравновесных процессов.

И (6), (8) следует, также, что

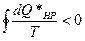(9)

Действительно это так, поскольку интегрировать надо разность (5), а она отрицательна. Объединяя (2) и (9) имеем

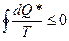(10)

неравенство Клаузиуса, причём равенство имеет место только для равновесных процессов. Это неравенство означает, что невозможно вернуть систему (например – рабочее тело тепловой машины) не отнимая от него тепла. Из (7), кроме того, следует, что для того, чтобы система совершила максимальную работу, надо чтобы процесс был максимально близко к обратимому, равновесному, квазистатическому.

Цикл Карно

Какую максимальную работу можно совершить за счёт передачи тепла при круговом процесс? При этом рабочее тело должно не только получать, но и отдавать тепло.

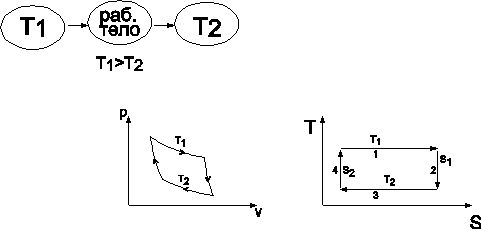
Согласно неравенству (10) нужен квазистатический процесс. Рассмотрим цикл Карно – две адиабаты и две изотермы.

Определим КПД как 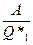(отношение работы к полученному теплу). За полный цикл 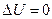, и согласно I-ому началу термодинамики, 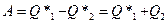, где Q₂ – количество теплоты, отданное второму термостату (холодильнику). На адиабатических плечах dQ*=0 и, согласно (2) 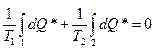, или

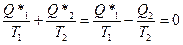
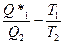, а КПД вводится как 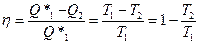(11)

КПД цикла Карно зависит только от температуры нагревателя и холодильника, и не зависит от рабочего тела (первая теорема Карно). Температура холодильника сильнее влияет, чем температура нагревателя. Можно показать, взяв 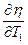и 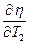, учтя, что T₁>T₂. Но T₂>0 (иначе КПД > 1 J).

Кроме того:

1) T₂=0 невозможно по III-му началу термодинамики.

2) цикл Карно имеет максимальный КПД. Это можно доказать;

3) Если хотя бы один из участков цикла необратимый, то, согласно неравенству Клаузиуса, 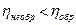(вторая теорема Карно).