Функция распределения системы с переменным числом частиц в термостате.

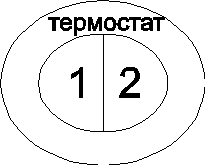
Посмотрим, как изменится функция распределения (каноническое распределение), если возможен обмен частицами системы с термостатом. Опыт:

N₁<<N₂, H₂>> H₁.

Здесь отметим, что при термодинамическом подходе под N понимается среднее число частиц систем. В статистике возможны флуктуации при переходе от одной системы к другой. Пусть полная система (система 1 + система 2 (термостат)) – изолирована, и

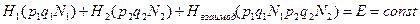, (11)

причём 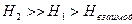, E = U – внутренняя энергия всей системы,

N₁ + N₂ = const = N₀. (12)

Очевидно теперь, что микроканоническое распределение будет иметь следующий вид:

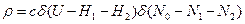(13)

Найдём 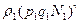- вероятность найти систему 1 в состоянии p₁,q₁,N₁ при всех возможных состояниях термостата.

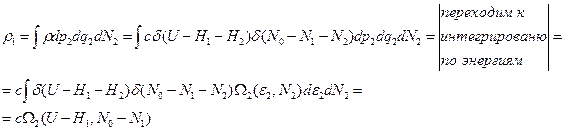(14)

Теперь естественно статистический вес зависит от числа частиц в системе (N₀-N₁), а это число в свою очередь определяет размерность фазового объёма. При N₂=const, из (14) должно получаться каноническое распределение (например в виде (29)) (это - непроницаемая стенка). Поэтому сейчас просто представим 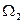в виде:

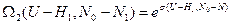
и поскольку H₁<<U и N₁<<N₀ – раскладываем в ряд:

,

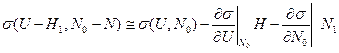Далее из этих соотношений можем записать (индекс 1 опускаем):

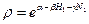(15)

При 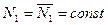, непроницаемые стенки из (15) должны иметь (см 29 формулу):

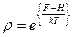. (16)

Поэтому (15) представим в виде:

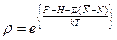(17)

(17) даёт (16) при 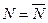, а зависимость от N – линейная, согласно (15).

Предположим, что 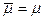- хим.потенциал. Тогда 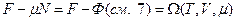. Условие нормировки для (17), (14) :

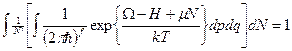(18)

Вообще говоря, 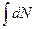нехорошо, т.к. N – дискретно. Но т.к. N>>1, т.е. N=0, - весьма условно, а также число частиц очень большое – переходим в пределе от суммирования к интегрированию.

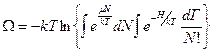(19)

Возьмём 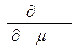, при T = const и V = const:

,

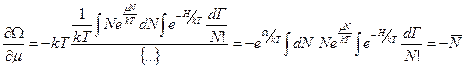Теперь вспомним термодинамическое соотношение (10) – совпадает с первой формулировкой, значит 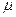- действительно хим. потенциал.

Итак:

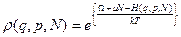(20)

- большое каноническое распределение Гиббса.

Некоторые свойства этого распределения:

Если систему в термостате разделить на две части, то

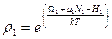
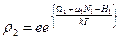
(T₁=T₂=T). Пренебрегая H_взаимн имеем:

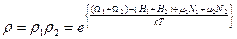, т.е. , , , ,

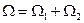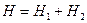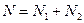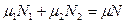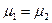
Кроме того, из общего условия нормировки f=f₁+f₂, действительно

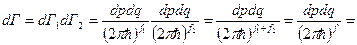
Это большое каноническое распределение Гиббса описывает системы не только с переменной (флук.) энергией, но и с переменным числом частиц.

§ Распределение Максвелла.

Распределение нам уже знакомо, вопрос в том, как можно получить его из распределения Гиббса?

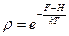(считаем N=const)

или 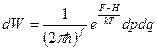(1)

- вероятность найти систему в состоянии p,q. Гамильтониан

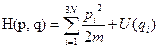(2)

(первое слагаемое – кинетическая энергия, второе – потенциальная, внешних полей +энергия взаимодействия);Формула (2) – для простых систем. На самом деле здесь – обобщённые импульсы. Подставим (2) → (1)

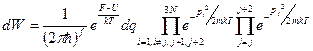(3)

Отсюда следует, что вероятность найти одну (j-ую, любую) частицу, в интервале импульсов от p до dp. (или в декартовой системе координат (j опускаем без потери общности) от p_x до p_x+dp_x,… не зависит от остальных и равна:

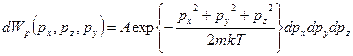(4)

Здесь в (4) выбрана 1 частица, остальные характеристики системы находятся в константе А, которую проще всего найти из нормировки 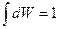. (4) – распределение Максвелла.

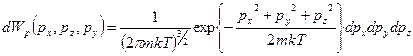(5)

Переходим к распределению по скоростям.

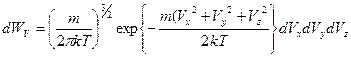(6)

- справедливо для распределения частиц любого сорта в термодинамическом равновесии (электроны, ионы, атомы, молекулы) со скоростью, меньше скорости света.

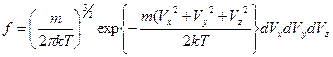(7)

- одночастичная функция распределения Максвелла.