Система с переменным числом частиц. Термодинамический подход.
До сих пор молча предполагали, что число частиц в системе N неизменно. Кроме последней лекции, где наткнулись на парадокс. Из-за чего может меняться число частиц? Открытая система (жидкость в контакте с паром), химические реакции в системе «рождение » (излучение) и «смерть» (поглощение) квантов (равновесное излучение) и т.д.
В этом случае формулировка 0-го начала термодинамики должна быть видоизменена: состояние (внутренние параметры) равновесной системы определяются температурой, внешними параметрами, а также числом частиц в системе.
Внутренняя энергия системы будет меняться за счёт изменения числа частиц в системе и I-ое начало надо записать в следующем виде:
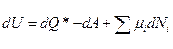 (1)
(1)
где Ni – число частиц сорта “i”, 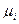 - соответствующий коэффициент (функция), определяющий изменение внутренней энергии при увеличении числа частиц на 1. Следует отметить, что у нас термодинамический подход, и значит под Ni надо понимать средне число частиц.
- соответствующий коэффициент (функция), определяющий изменение внутренней энергии при увеличении числа частиц на 1. Следует отметить, что у нас термодинамический подход, и значит под Ni надо понимать средне число частиц.
Для квазистатических процессов выражение (1) записывается следующим образом (это новое основное уравнение):
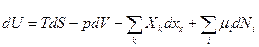 (2)
(2)
и 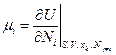 - химический потенциал частиц сорта i. С помощью основного уравнения (2) нетрудно найти, что
- химический потенциал частиц сорта i. С помощью основного уравнения (2) нетрудно найти, что
F = U-TS - свободная энергия, энергия Гельмгольца.
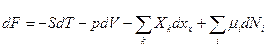 (3)
(3)
Ф – термодинамический потенциал, энергия Гиббса;
Ф = F+pV = U - TS + pV;
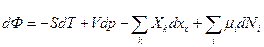 (4)
(4)
I = U + pV – энтальпия.
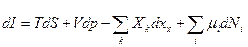 (5)
(5)
Отсюда видно, что
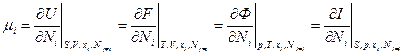 (6)
(6)
и химический потенциал можно получить дифференцированием любой из переменных по Ni, однако каждый раз – разные независимые переменные.
Все характеристические функции – аддитивны (уже знаем; павда только с точностью жо энергии взаимодействия). Поэтому для системы с одним сортом частиц N при изменении их числа все характеристические функции меняются в одинаковое число раз N.
Замечание: переменные T и p – аддитивны во всей равновесной системе и нельзя ввести «удельную» температуру или «удельное» давление на одну частицу. Энергия, объём и другие – для них можно.
Итак:
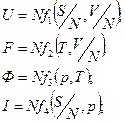 ,
,
а химический потенциал 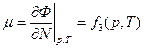 - равен термодинамическому потенциалу на одну частицу (
- равен термодинамическому потенциалу на одну частицу ( 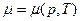 и е зависит от числа частиц N).
и е зависит от числа частиц N).
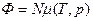 (7)
(7)
Если имеются разные сорта частиц (смесь), то аддитивность характеристических функций не выполняется (так как между частицами может быть сильное взаимодействие; исключение может составить разве что смесь идеальных газов, где не учитывается взаимодействие частиц). Однако (7) можно обобщить на любую смесь, т.е.
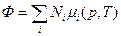 (7`)
(7`)
Действительно, так как T и p - интенсивные параметры (одинаковы для всей системы), от N не зависит), N – экстенсивный, (аддитивный), то
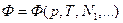
Положим 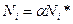 (изменение числа частиц Ni в
(изменение числа частиц Ni в 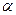 раз, или число грамм-молей
раз, или число грамм-молей 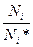 ), тогда
), тогда 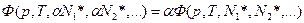 (получается с учётом линейности и аддитивности при одинаковых
(получается с учётом линейности и аддитивности при одинаковых 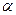 . Возьмём
. Возьмём 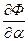 :
:
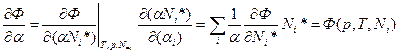
С другой стороны, Ni* - произвольное, не обязательно фиксированное чем-то число частиц, и можно положить 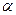 = 1. Тогда получаем (* - опускаем из написания):
= 1. Тогда получаем (* - опускаем из написания):
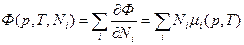 (7``)
(7``)
При изучении частиц с переменным числом частиц полезно ввести новую характеристическую функцию, дифференцирование которой по независимым переменным позволяет найти число частиц разного сорта.
Возьмём (3) и 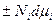 , получаем:
, получаем:
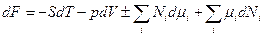 (8)
(8)
Но из (7`) 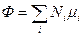 , и
, и
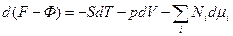 (9)
(9)
где 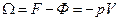 - большой термодинамический потенциал и
- большой термодинамический потенциал и
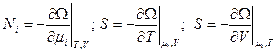 (10)
(10)
Дата добавления: 2021-05-28; просмотров: 696;











