Уравнение динамики вращательного движения

Твердого тела

Пусть материальная точку массой m, движущуюся по окружности радиусом r под действием постоянной силы F направленная по касательной к окружности. Согласно второму закону Ньютона, эта сила вызывает тангенциальное ускорение

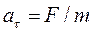или

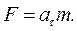
Используя соотношение, связывающее тангенциальное и угловое ускорение ε

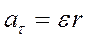получаем

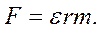
Умножим обе части написанного выше равенства на r:

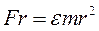(5.14)

Левая часть выражения (5.14) является моментом силы: .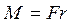

Правая часть представляет собой произведение углового ускорения ε на момент инерции материальной точки А.

Так как твердое тело представляет систему неподвижно связанных между собой материальных точек, а для каждой из них справедливо соотношение (5.14), то

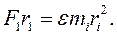
Тогда

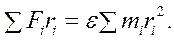
Обозначая 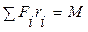— суммарный вращающий момент, а

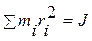— момент инерции твердого тела относительно оси О'О', получаем основное уравнение динамики вращательного движения твердого тела:

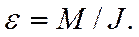(5.15)

Угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

При постоянном моменте вращающей силы угловое ускорение будет величиной постоянной и его можно выразить через разность угловых скоростей:

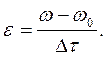(5.16)

Тогда основное уравнение динамики вращательного движения можно записать в виде

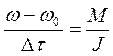или 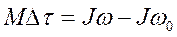(5.17)

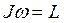—момент импульса (или момент количества движения), МΔτ — импульс момента сил (или импульс вращающего момента).

Эти величины векторные и совпадают по направлению с векторам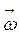и и .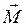

Определим кинетическую энергию твердого тела, вращающегося вокруг неподвижной оси. Разобьем это тело на n материальных точек. Каждая точка движется с линейной скоростью 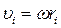, тогда кинетическая энергия точки

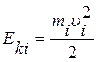или 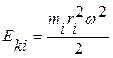. (5.18)

Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:

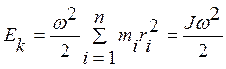(5.19)

[J— момент инерции тела относительно оси вращения].

Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна

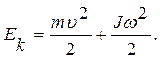(5.20)

Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела.

Рассмотрим, например скатывание шара по наклонной плоскости с высоты h без проскальзывания с начальной нулевой скоростью (рисунок 5.4). Найдем скорость перемещения шара в конце спуска. Из закона сохранения энергии

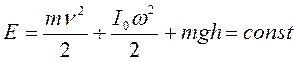
имеем:

.

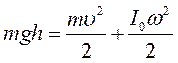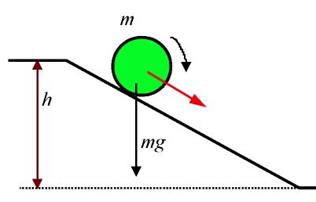
Рисунок 5.4 – Скатывание шара с наклонной плоскости.

Условие движения без проскальзывания означает, что линейная скорость центра масс связана с угловой скоростью 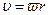, момент инерции шара равен

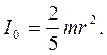
Тогда искомая скорость шара в конце спуска:

<11 12 131415 16 17 >

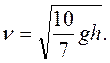
Дата добавления: 2017-01-08; просмотров: 6079;