Закон сохранения энергии в механике

Количественную формулировку закона сохранения и превращения энергии дали немецкие ученые Ю. Майер и Г. Гельмгольц (XIX в.): в замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.

Закон сохранения и превращения энергии является одним из фундаментальных законов природы, справедливым как для систем макроскопических тел, так и для систем элементарных частиц.

В замкнутой системе тел, силы взаимодействия между которыми консервативны (потенциальны), отсутствуют взаимные превращения механической энергии в другие виды энергии. Такие системы называются замкнутыми консервативными и для них справедлив закон сохранения энергии в механике: механическая энергия замкнутой консервативной системы не изменяется в процессе ее движения:

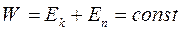(4.16)

Для вывода этого закона рассмотрим систему материальных точек максами m₁, m₂, … , m_n, движущихся со скоростями 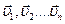. Пусть 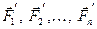- равнодействующие внутренних консервативных сил, действующие на каждую из этих точек, а 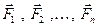- равнодействующие внешних сил, которые также будем считать консервативными. 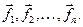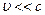Кроме того, будем считать, что на материальные точки действует еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим При массы материальных точек постоянны и уравнения движения этих точек по второму закону Ньютона имеют следующий вид:

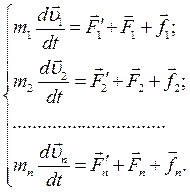(4.17)

Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения 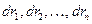. Умножим каждое уравнение системы (4.17) на соответствующее перемещение:

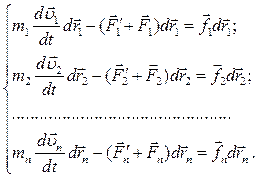
Учитывая, что 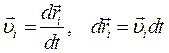, получим:

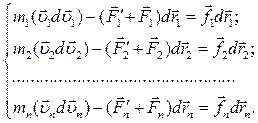
Складывая эти уравнения, получим:

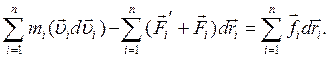(4.18)

Первый член левой части (3.13) представляет собой приращение кинетической энергии системы:

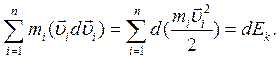
Второй член 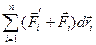равен элементарной работе внутренних и внешних консервативных сил, т.е. равен элементарному приращению потенциальной энергии dE_п.

Правая часть уравнения (6.18) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем:

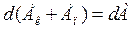(4.19)

При переходе системы из состояния 1 в какое-либо состояние 2

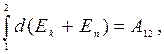
т.е изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (4.19) следует, что

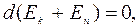
откуда

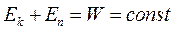, (4.20)

что и требовалось доказать.

Из равенства (4.20) следует, чтосумма кинетической и потен­циальной энергии тел, составляю­щих замкнутую систему, в которой действуют консервативные силы, остается постоянной.Это утверж­дение называется законом сохра­нения энергии в механических процессах.

Для любой замкнутой системы всегда выполняется закон сохранения и превращения энергии: полная энергия замкнутой системы остается постоянной. При этом, будучи несозидаемой и неуничтожаемой, энергия может превращаться из одного вида в другой.

Не сохраняется полная механическая энергия и в том случае, если в системе тел происходят неупругие деформации. Но убывание механичес­кой энергии не означает, что энергия исчезает бесследно. Она превраща­ется из механической в другую, в частности во внутреннюю энергию.

Внутренняя энергия тела – энергия, связанная с движением молекул, из которых состоит тело, и их взаимодействием между собой. Пока (при изучении механики) это качественное определение, которое будет конкретизировано при изучении термодинамики.