Законы Кеплера и закон всемирного тяготения

<13 14 151617 18 19 >

В мире атомов и элементарных частиц гравитационные силы пренебрежимо малы по сравнению с другими видами силового взаимодействия между частицами. Очень непросто наблюдать гравитационное взаимодействие и между различными окружающими нас телами, даже если их массы составляют многие тысячи килограмм. Однако именно гравитация определяет поведение «больших» объектов, таких, как планеты, кометы и звезды, именно гравитация удерживает всех нас на Земле.

Гравитация управляет движением планет Солнечной системы. Без нее планеты, составляющие Солнечную систему, разбежались бы в разные стороны и потерялись в безбрежных просторах мирового пространства.

Закономерности движения планет с давних пор привлекали внимание людей. Изучение движения планет и строения Солнечной системы и привело к созданию теории гравитации – открытию закона всемирного тяготения.

С точки зрения земного наблюдателя планеты движутся по весьма сложным траекториям. Первая попытка создания модели Вселенной была предпринята Птолемеем. В центре мироздания Птолемей поместил Землю, вокруг которой по большим и малым кругам, как в хороводе, двигались планеты и звезды.

Геоцентрическая система Птолемея продержалась более 14 столетий и только в середине XVI века была заменена гелиоцентрической системой Коперника. В системе Коперника траектории планет оказались более простыми.

Немецкий астроном И. Кеплер в начале XVII века на основе системы Коперника сформулировал три эмпирических закона движения планет Солнечной системы. Кеплер использовал результаты наблюдений за движением планет датского астронома Т. Браге.

Первый закон Кеплера(1609 г.):Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

На рисунке 6.1 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удаленная от Солнца, называется афелием или апогеем. Расстояние между афелием и перигелием – большая ось эллипса.

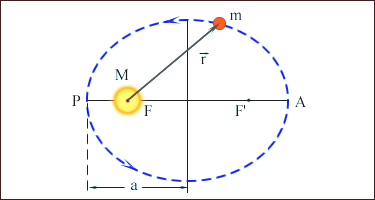
Рисунок 6.1 – Эллиптическая орбита планеты массой m << M.

а – длина большой полуоси, F и F' – фокусы орбиты.

Почти все планеты Солнечной системы (кроме Плутона) движутся по орбитам, близким к круговым.

Второй закон Кеплера(1609 г.):Радиус-вектор планеты описывает в равные промежутки времени равные площади.

Иллюстрация второго закона Кеплера, который иногда называется законом площадей, приведена на рисунке 6.2.

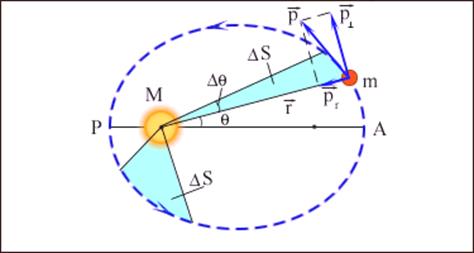
Рисунок 6.2 – Закон площадей – второй закон Кеплера.

Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рисунке 6.2 изображен вектор импульса тела 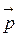и его составляющие 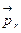и 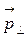Площадь, заметенная радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием rΔθ и высотой r:

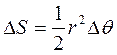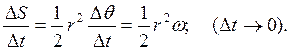или (6.1)

Здесь 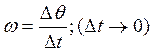– угловая скорость.

Момент импульса L по абсолютной величине равен произведению модулей векторов 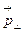и 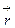: 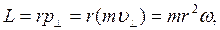так как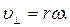

Из этих отношений следует:

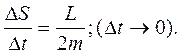(6.2)

Поэтому, если по второму закону Кеплера 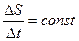, то и момент импульса L при движении остается неизменным. В частности, поскольку скорости планеты в перигелии и афелии направлены перпендикулярно радиус-векторам 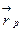и 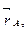из закона сохранения момента импульса следует:

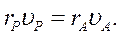
Третий закон Кеплера (1619 г.): Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:

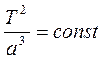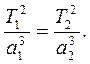или (6.3)

Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью порядка 1 %.

На рисунке 6.3 изображены две орбиты, одна из которых круговая с радиусом R, а другая – эллиптическая с большой полуосью a. Третий закон утверждает, что если R = a, то периоды обращения тел по этим орбитам одинаковы.

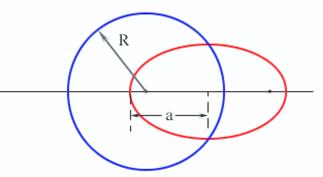
Рисунок 6.3 – Круговая и эллиптическая орбиты.

Несмотря на то, что законы Кеплера явились важнейшим этапом в понимании движения планет, они все же оставались только эмпирическими правилами, полученными из астрономических наблюдений. Законы Кеплера нуждались в теоретическом обосновании. Решающий шаг в этом направлении был сделан Исааком Ньютоном, открывшим в 1682 году закон всемирного тяготения:

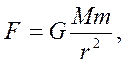(6.4)

где M и m – массы Солнца и планеты, r – расстояние между ними, G = 6,67·10–11 Н·м²/кг² – гравитационная постоянная. Ньютон первый высказал мысль о том, что гравитационные силы определяют не только движение планет Солнечной системы; они действуют между любыми телами Вселенной. В частности, сила тяжести, действующая на тела вблизи поверхности Земли, имеет гравитационную природу.

Для круговых орбит первый и второй закон Кеплера выполняются автоматически, а третий закон утверждает, что T² ~ R³, где Т – период обращения, R – радиус орбиты. Отсюда можно получить зависимость гравитационной силы от расстояния. При движении планеты по круговой траектории на нее действует центростремительная сила, которая возникает за счет гравитационного взаимодействия планеты и Солнца:

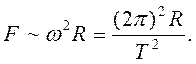(6.5)

Если T² ~ R³, то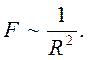

Свойство консервативности гравитационных сил позволяет ввести понятие потенциальной энергии. Для сил всемирного тяготения удобно потенциальную энергию отсчитывать от бесконечно удаленной точки.

Потенциальная энергия тела массы m, находящегося на расстоянии r от неподвижного тела массы M, равна работе гравитационных сил при перемещении массы m из данной точки в бесконечность.

Математическая процедура вычисления потенциальной энергии тела в гравитационном поле состоит в суммировании работ на малых перемещениях (рисунок 6.4).

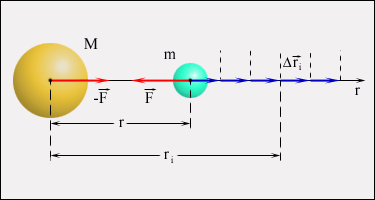
Рисунок 6.4 – Вычисление потенциальной энергии тела в гравитационном поле.

Закон всемирного тяготения применим не только к точеным массам, но и к сферически симметричным телам. Работа ΔA_i гравитационной силы 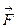на малом перемещении 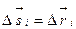есть:

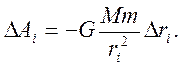(6.6)

Полная работа при перемещении тела массой m из начального положения в бесконечность находится суммированием работ ΔAi на малых перемещениях: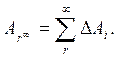

В пределе при Δr_i → 0 эта сумма переходит в интеграл. В результате вычислений для потенциальной энергии получается выражение

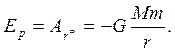(6.7)

Знак «минус» указывает на то, что гравитационные силы являются силами притяжения.

Если тело находится в гравитационном поле на некотором расстоянии r от центра тяготения и имеет некоторую скорость υ, его полная механическая энергия равна

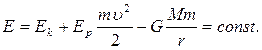(6.8)

В соответствии с законом сохранения энергии полная энергия тела в гравитационном поле остается неизменной.

Полная энергия может быть положительной и отрицательной, а также равняться нулю. Знак полной энергии определяет характер движения небесного тела (рисунок 6.5).

При E = E₁ < 0 тело не может удалиться от центра притяжения на расстояние r > r_max. В этом случае небесное тело движется по эллиптической орбите (планеты Солнечной системы, кометы).

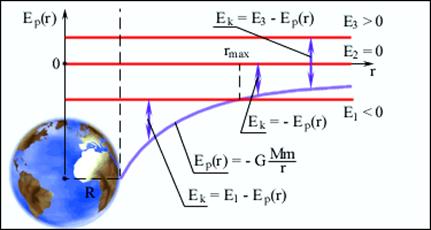
Рисунок 6.5 – Диаграмма энергий тела массой m в гравитационном поле,

создаваемом сферически симметричным телом массой M и радиусом R.

При E = E₂ = 0 тело может удалиться на бесконечность. Скорость тела на бесконечности будет равна нулю. Тело движется по параболической траектории.

При E = E₃ > 0 движение происходит по гиперболической траектории. Тело удаляется на бесконечность, имея запас кинетической энергии.

Законы Кеплера применимы не только к движению планет и других небесных тел в Солнечной системе, но и к движению искусственных спутников Земли и космических кораблей. В этом случае центром тяготения является Земля.

Первой космической скоростью называется скорость движения спутника по круговой орбите вблизи поверхности Земли. Из второго закона ньютона для данного случая:

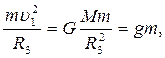
следует 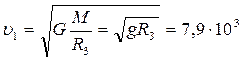м/с. (6.9)

Второй космической скоростью называется минимальная скорость, которую нужно сообщить космическому кораблю у поверхности Земли, чтобы он, преодолев земное притяжение, превратился в искусственный спутник Солнца (искусственная планета). При этом корабль будет удаляться от Земли по параболической траектории. Из выражения

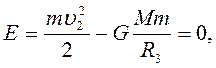
следует

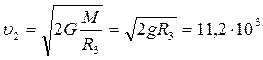м/с. (6.10)

<13 14 151617 18 19 >

Дата добавления: 2017-01-08; просмотров: 7434;