Консервативные и неконсервативные силы

Все силы, встречающиеся в механике макроскопических тел, принято разделять на консервативные и неконсервативные. Консервативными называются силы, работа которых не зависит от формы пути между двумя точками (при перемещении тела между ними).

Примером консервативных сил является, например, сила тяжести. Вычислим работу этой силы при переходе материальной точки из положения 1 в положение 2 вдоль прямолинейного отрезка r₁₂:

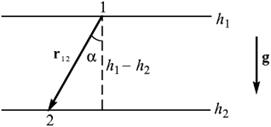
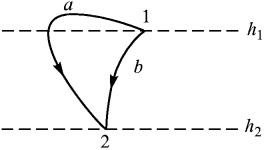
Рисунок 4.3 – К определению работы силы тяжести

A₁₂ = mg· r₁₂ = mgr₁₂cosα = mg(h₁–h₂) = mgh₁–mgh₂, (4.13)

где h₁ и h₂ — высоты, на которых находилась материальная точка в начале и в конце пути. Они отсчитываются от какого-либо произвольного уровня, например от земной поверхности или от уровня моря.

Формула для работы 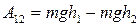остается справедливой и при перемещении вдоль произвольной кривой 1a2 или 1b2 (рисунок .3).

Для доказательства этого утверждения надо разбить весь путь горизонтальными плоскостями на малые участки, каждый из которых может быть принят за прямолинейный. Применив к каждому участку выведенную формулу 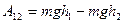и сложив полученные работы, мы придем к прежнему результату. Таким образом, работа силы тяжести не зависит от формы пути. Она определяется только начальным и конечным положениями перемещающейся точки.

Кроме того, сравнивая

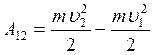и

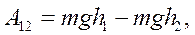
приходим к выводу, что

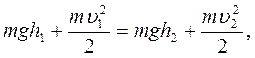
то есть при движении в поле силы тяжести сохраняется величина

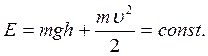(4.14)

Она, как вы знаете, называется полной энергией системы и складывается из кинетической и потенциальной энергии. Под потенциальной энергией здесь надо понимать величину .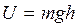

Вторым примером консервативных сил являются так называемые центральные силы.

Примером таких сил могут служить силы гравитационного притяжения Земли к Солнцу (или Луны к Земле)..

Покажем, что работа центральных сил также не зависит от формы пути и определяется только начальным и конечным положениями материальной точки (рисунок 4.4). Для этого произведем бесконечно малое перемещение .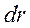

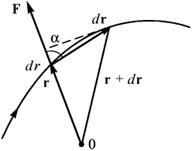
Рисунок 4.4 – К определению работы центральных сил

При этом

,

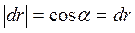где 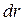— приращение расстояния до центра (рисунок 4.4). Таким образом, 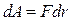и

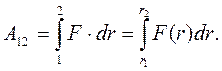(4.15)

Значение определенного интеграла зависит только от нижнего и верхнего пределов 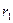и 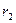и, таким образом, не зависит от формы пути.

Все силы, не являющиеся консервативными, называются неконсервативными силами. К ним относятся, прежде всего, так называемые диссипативные силы, например силы трения, возникающие при скольжении одного тела относительно другого.

Сила трения в этом случае всегда направлена против скорости движения, то есть против перемещения тела. Работа этой силы всегда отрицательна. И если тело сместилось налево, а потом вернулось назад, то очевидно, что суммарная работа будет величиной отрицательной и не равной нулю. Таким образом, работа силы трения скольжения при движении по замкнутому контуру не равна нулю!

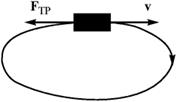
Рисунок 4.5 – Работа силы трения на замкнутом контуре

К неконсервативным силам относятся также силы сопротивления, которые действуют на тело при его движении в жидкой или газообразной среде. Эти силы называют иногда силами вязкого трения. В отличие от трения скольжения, они всегда зависят от абсолютной величины скорости тела и направлены противоположно ей.